週期位能所帶來的能帶結構——Bloch’s Theorem

在各種物質形態中，固態顯然是比液態甚至是氣態還要有序許多的型態。因此，固態理論發展得較為成熟，倒也不是什麼意外的事。而固態的特點就在於具有週期的晶格排列。

$$U(\mathbf{r}+\mathbf{R})=U(\mathbf{r})\label{1}\tag{1}$$

由於我認為固態物理的精華，以及半導體物理的基礎就在於能帶概念。了解能帶結構（Band structure），才有可能了解能帶圖（Band diagram），因此將我對於 Ashcroft & Mermin (1976) 的讀書心得整理為這篇文章，逐一說明下述觀念：

• 布拉赫定理（Bloch’s theorem）
• 布拉赫定理的第一種證明
• 波恩・馮卡曼邊界條件（Born-von Karman Boundary Condition）
• 布拉赫定理的第二種證明
• 布拉赫定理的物理內涵

希望讀者們在看完這篇文章後，就能了解：

• 倒空間（reciprocal space）的晶格點（Bloch wave vector）是怎麼來的？
• 為什麼晶格點並不像實數軸那樣連續？它們之間的最小間隔是怎麼來的？
• 什麼是晶格動量（Crystal momentum）？為什麼有這種概念？
• 到底能帶結構（Band structure）$\varepsilon_{n}(\mathbf{k})$是怎麼來的？

---

布拉赫定理（Bloch’s theorem）

固體中的電傳導問題本質上是個多電子問題（many-electron problem），因此電位能 $U(\mathbf{r})$ 除了應考慮電子（electron）與原子核（nuclie）之間的電位能 $U_\text{e,n}(\mathbf{r})$ 以外，還應該考慮電子與電子之間的電位能 $U_\text{e,e}(\mathbf{r})$。然而，不論你考慮的位能有多全面，基本上我們在此僅處理週期位能。換言之，底下的討論適用於任何滿足週期條件 Eq.$(\ref{1})$ 的位能形式。僅僅這個“週期性質”，就能帶給我們非常多的物理結論。

具體來說，在此我們說，每個電子都滿足底下的薛丁格方程式：

$$H\psi=\left[-\frac{\hbar^2}{2m}\nabla^2+U(\mathbf{r})\right]\psi=\varepsilon\psi\label{2}\tag{2}$$

其中，$U(\mathbf{r})$ 滿足 Eq.$(\ref{1})$。所謂的“自由電子”（free electron）就是指 $U(\mathbf{r})=0$，也就是最簡單的“週期位能”。此外，所謂的“布拉赫電子”（Bloch electron）就是具有週期位能 Eq.$(\ref{1})$ 且具有 Eq.$(\ref{2})$ 單電子形式的薛丁格方程式的電子。

對於所有位於布拉菲晶格（Bravais lattice）的 $\mathbf{R}$ 而言，具有週期位能 $U(\mathbf{r})=U(\mathbf{r}+\mathbf{R})$ 的單電子哈米爾頓（Hamiltonian） $H=-\hbar^2\nabla^2/2m+U(\mathbf{r})$，其特徵態（eigenstate）能夠被寫為平面波與具有布拉菲晶格週期的函數：

$$\psi_{n\mathbf{k}}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_{n\mathbf{k}}(\mathbf{r})\tag{3}\label{3}$$

其中，對於所有位於布拉菲晶格的 $\mathbf{R}$，

$$u_{n\mathbf{k}}(\mathbf{r})=u_{n\mathbf{k}}(\mathbf{r}+\mathbf{R})\tag{4}\label{4}$$

布拉赫定理的第一形式

以上即為布拉赫定理的第一種形式。此外，基於 Eq.$(\ref{3})$、Eq.$(\ref{4})$，我們可推得：

$$\psi_{n\mathbf{k}}(\mathbf{r}+\mathbf{R})=e^{i\mathbf{k}\cdot\mathbf{R}}\psi_{n\mathbf{k}}(\mathbf{r})\tag{5}\label{5}$$

因此，有時布拉赫定理也會改用 Eq.$(\ref{5})$ 來表示：

對於每個 $H$ 的特徵態 $\psi$ 而言，總是存在著一個波向量 $\mathbf{k}$，使得對於所有位於布拉菲晶格的 $\mathbf{R}$ 而言，

$$\psi_{n\mathbf{k}}(\mathbf{r}+\mathbf{R})=e^{i\mathbf{k}\cdot\mathbf{R}}\psi_{n\mathbf{k}}(\mathbf{r})\tag{6}\label{6}$$

布拉赫定理的第二形式

布拉赫定理的第一種證明

首先我們對於每個布拉菲晶格向量（Bravais lattice vector）$\mathbf{R}$，定義相對應的平移算符（translation operator）$T_\mathbf{R}$，使得每當此算符作用於任何一個函數 $f(\mathbf{r})$ 後，就會生成其圖像被平移 $\mathbf{R}$ 的新函數：

$$T_\mathbf{R}f(\mathbf{r})=f(\mathbf{r}+\mathbf{R})\tag{7}\label{7}$$

接著，由於我們目前考慮的位能具有週期性，所以目前的哈密頓算符也具有週期性，$H(\mathbf{r})=H(\mathbf{r}+\mathbf{R})$，因此：

$$T_\mathbf{R}H\psi=H(\mathbf{r}+\mathbf{R})\psi(\mathbf{r}+\mathbf{R})=H(\mathbf{r})\psi(\mathbf{r}+\mathbf{R})=HT_\mathbf{R}\psi\tag{8}\label{8}$$

由於 Eq.$(\ref{8})$ 適用於任何波函數 $\psi$，所以我們有底下的恆等式：

$$T_\mathbf{R}H=HT_\mathbf{R}\tag{9}\label{9}$$

除此之外，對於任何一個 $\psi(\mathbf{r})$，不論它先平移 $\mathbf{R}$ 還是 $\mathbf{R}^\prime$，其結果都是一樣的：

$$T_\mathbf{R}T_{\mathbf{R}^\prime}\psi(\mathbf{r})=T_{\mathbf{R}^\prime}T_\mathbf{R}\psi(\mathbf{r})=\psi(\mathbf{r}+\mathbf{R}+\mathbf{R}^\prime)\tag{10}\label{10}$$

因此，我們可以定義 $T_{\mathbf{R}+\mathbf{R}^\prime}$：

$$T_{\mathbf{R}+\mathbf{R}^\prime}\equiv T_\mathbf{R}T_{\mathbf{R}^\prime}=T_{\mathbf{R}^\prime}T_\mathbf{R}\tag{11a}\label{11a}$$

$$T_{\mathbf{R}+\mathbf{R}^\prime}\psi(\mathbf{r})=\psi(\mathbf{r}+\mathbf{R}+\mathbf{R}^\prime)\tag{11b}\label{11b}$$

由 Eq.$(\ref{9})$、Eq.$(\ref{11a})$ 我們可知，所有布拉菲晶格 $\mathbf{R}$ 的平移算符 $T_\mathbf{R}$ 與 Hamiltonian $H$，任何兩者彼此都是“可交換的”（commuting operators）。因此，根據可對易觀察量之完備集（Complete set of commuting observables）的相容性定理（the compatibility theorem），我們可知 $H$ 的特徵態能夠同時是所有 $T_\mathbf{R}$ 的特徵態：

$$H\psi=\varepsilon\psi\tag{12a}\label{12a}$$

$$T_\mathbf{R}\psi=c(\mathbf{R})\psi\tag{12b}\label{12b}$$

而根據 Eq.$(\ref{10})$、Eq.$(\ref{11a})$，我們可知各平移算符 $T_\mathbf{R}$ 的特徵值並非相互獨立的：

$$T_\mathbf{R}T_{\mathbf{R}^\prime}\psi=c(\mathbf{R}^\prime)T_\mathbf{R}\psi=c(\mathbf{R}^\prime)c(\mathbf{R})\psi\tag{13a}\label{13a}$$

$$T_{\mathbf{R}+\mathbf{R}^\prime}\psi=c(\mathbf{R}+\mathbf{R}^\prime)\psi\tag{13b}\label{13b}$$

因此，

$$c(\mathbf{R}+\mathbf{R}^\prime)=c(\mathbf{R})c(\mathbf{R}^\prime)\tag{14}\label{14}$$

基於 Eq.$(\ref{14})$ 的特性，我們可以開始做些假設。首先，由於布拉菲晶格的原初向量（primitive vectors）$\mathbf{a}_i$ 當然是一種布拉菲晶格向量，即 $\mathbf{a}_i\in\mathbf{R}$，也就必然滿足 Eq.$(\ref{14})$：

$$c(\mathbf{a}_i+\mathbf{a}_j)=c(\mathbf{a}_i)c(\mathbf{a}_j)\tag{15}\label{15}$$

而這種「由相加轉為相乘」的函數，最典型的莫過於指數函數了，因此我們將 $c(\mathbf{a}_i)$ 進一步用“複數” $x_i$ 寫為（待會可證明 $x_i$ 必須屬於實數）：

$$c(\mathbf{a}_i)=e^{2\pi ix_i}\tag{16}\label{16}$$

因此，倘若 $\mathbf{R}$ 是布拉菲晶格向量，那麼必然可表示為：

$$\mathbf{R}=n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\tag{17}\label{17}$$

將 Eq.$(\ref{17})$ 代入 Eq.$(\ref{14})$，可以得到：

$$\begin{align}c(\mathbf{R})&=c(n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3)\tag{18a}\label{18a}\\[5pt]&=c(n_1\mathbf{a}_1)c(n_2\mathbf{a}_2+n_3\mathbf{a}_3)\tag{18b}\label{18b}\\[5pt]&=c(n_1\mathbf{a}_1)c(n_2\mathbf{a}_2)c(n_3\mathbf{a}_3)\tag{18c}\label{18c}\\[5pt]&=c(\underbrace{\mathbf{a}_1+\mathbf{a}_1+\cdots}_{n_1\mathbf{a}_1})c(n_2\mathbf{a}_2)c(n_3\mathbf{a}_3)\tag{18d}\label{18d}\\[5pt]&=c(\mathbf{a}_1)^{n_1}c(\mathbf{a}_2)^{n_2}c(\mathbf{a}_3)^{n_3}\tag{18e}\label{18e}\end{align}$$

而很巧的是，從 Eq.$(\ref{16})$ 與 Eq.$(\ref{18e})$，我們不難發現 $c(\mathbf{R})$ 其實可依照 Eq.$(\ref{16})$ 的由來，進一步改寫為：

$$c(\mathbf{R})=e^{i\mathbf{k}\cdot\mathbf{R}}\tag{19}\label{19}$$

其中，

$$\mathbf{k}\equiv x_1\mathbf{b}_1+x_2\mathbf{b}_2+x_3\mathbf{b}_3\tag{20}\label{20}$$

並且 $\mathbf{b}_i$ 即滿足 $\mathbf{b}_i\cdot\mathbf{a}_j=2\pi\delta_{ij}$ 的倒晶格向量（reciprocal lattice vector）。最後，根據 Eq.$(12b)$，我們成功得到了布拉赫定理的第二形式。也就是說，對於任何具有週期位能的 Hamiltonian，我們總是能選擇適當的特徵態 $\psi$，使得對於所有布拉菲晶格 $\mathbf{R}$：

$$T_\mathbf{R}\psi(\mathbf{r})=\psi(\mathbf{r}+\mathbf{R})=c(\mathbf{R})\psi(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{R}}\psi(\mathbf{r})\tag{21}\label{21}$$

波恩・馮卡曼邊界條件

在由 Eq.$(\ref{15})$ 推到 Eq.$(\ref{16})$ 時，我們僅僅是因為它的「相加轉成相乘」的性質，而提出 $c(\mathbf{a}_i)=e^{2\pi ix_i}$ 的指數形式。因此，這裡的 $x_i$ 並不需要是實數，也可以是含有虛數 $i$ 的複數，之所以前方有著 $2\pi i$ 係數，完全是為了後續結論做準備。

目前我們的結論只有 Eq.$(\ref{6})$、Eq.$(\ref{21})$ 的布拉赫定理，$\psi(\mathbf{r}+\mathbf{R})=e^{i\mathbf{k}\cdot\mathbf{R}}\psi(\mathbf{r})$。滿足此性質的波函數有非常多種，但其實還必須施加上一個條件，最後留下的波函數才是我們所關心的。這條件就是很簡單的「波函數具有空間週期」的邊界條件。

然而，波函數的空間週期，是怎麼樣的呢？假設原子晶格常數為 $a$，那麼空間週期會是 $a$ 嗎？倘若 $\psi(x+a)=\psi(x)$，那麼就不可能有週期為 $2a$ 且 $\psi(x+a)\neq\psi(x)$ 的波函數了。然而，對我來說，這種波函數應該是可能的，畢竟想不到什麼理由不可能。以此類推，最後我們能推得的週期就會是在該維度（$x$）上的晶體距離，因為“比起晶體內部，表面上的波函數性質應該相去不遠”。假設此晶體在 $x_i$ 方向上的原子數目約有 $N_i$ 個，那麼可以得到：

$$\psi(\mathbf{r}+N_i\mathbf{a}_i)=\psi(\mathbf{r}),\quad i=1,2,3\tag{22}\label{22}$$

其中，$\mathbf{a}_i$ 為原初向量（primitive vector），並且 $N_i$ 為與原子總數立方根 $N^{1/3}$ 同數量級的整數，$N=N_1N_2N_3$ 為晶體中的原子總數。以上即為波恩・馮卡曼邊界條件（Born-Von Karman boundary condition）。

那麼施加此條件後，會有什麼理論結果呢？

根據 Eq.$(\ref{6})$、Eq.$(\ref{22})$，可以得到

$$\psi_{n\mathbf{k}}(\mathbf{r}+N_i\mathbf{a}_i)=e^{i\mathbf{k}_i\cdot N\mathbf{a}_i}\psi_{n\mathbf{k}}(\mathbf{r})=\psi_{n\mathbf{k}}(\mathbf{r})\tag{23}\label{23}$$

也就是說，

$$e^{i\mathbf{k}_i\cdot N\mathbf{a}_i}=1,\quad i=1,2,3\tag{24}\label{24}$$

緊接著，代入 Eq.$(\ref{20})$ 的 $\mathbf{k}$，可以得到

$$e^{2\pi iN_ix_i}=1,\quad i=1,2,3\tag{25}\label{25}$$

由此可得，

$$x_iN_i\in\mathbb{N}\quad\implies\quad m_i\equiv x_i N_i,\quad i=1,2,3,\quad m_i\in\mathbb{N}\tag{26}\label{26}$$

也就是說，$x_i$ 是個實數，並且是 $1/N_i$ 的整數倍！

$$x_i=\frac{1}{N_i},\frac{2}{N_i},\frac{3}{N_i},\cdots=\frac{m_i}{N_i},\quad i=1,2,3,\quad m_i\in\mathbb{N}\tag{27}\label{27}$$

以布拉赫定理而言，這告訴我們，布拉赫波向量（Bloch wave vector）的廣義形式為：

$$\mathbf{k}=\sum_{i=1}^3\frac{m_i}{N_i}\mathbf{b}_i,\quad m_i\in\mathbb{N}\tag{28}\label{28}$$

由 Eq.$(\ref{28})$ 可知，在 $\mathbf{k}$ 空間中的每個“波向量所佔據的微小體積” $\Delta \mathbf{k}$，即為由 $\mathbf{b}_i/N_i$ 所展開的平行六面體：

$$\Delta\mathbf{k}\equiv \frac{1\mathbf{b_1}}{N_1}\cdot\left(\frac{1\mathbf{b_2}}{N_2}\times\frac{1\mathbf{b_3}}{N_3}\right)=\frac{1}{N}\mathbf{b}_1\cdot\left(\mathbf{b}_2\times\mathbf{b}_3\right)\tag{29}\label{29}$$

由於 $\mathbf{b}_1\cdot\left(\mathbf{b}_2\times\mathbf{b}_3\right)$ 其實就是倒晶格的原初晶胞體積（volume of a reciprocal lattice primitive cell），所以 Eq.$(\ref{29})$ 相當於是在說，倒空間原初晶胞裡的波向量數目（allowed wave vector）等同於晶體中的原子總數。

最後，由於倒晶格的原初晶胞體積為 $(2\pi)^3/v$，其中 $v=V/N$，即直接晶格中的原初晶胞體積（direct lattice primitive cell），所以可進一步將 Eq.$(\ref{29})$ 改寫為：

$$\Delta\mathbf{k}=\frac{(2\pi)^3}{V}\tag{30}\label{30}$$

因此，對於具有週期位能的電子系統而言，除了會滿足布拉赫定理以外，其波向量 $\mathbf{k}$ 也會滿足 Eq.$(\ref{28})$ 的關係，即 Eq.$(\ref{20})$ 中的 $x_i=m_i/N_i, m_i\in\mathbb{N}$。

布拉赫定理的第二種證明

先前第一種證明是先從週期位能出發，得到布拉赫定理，接著再加上波恩・馮卡曼邊界條件。第二種證明則是先從滿足波恩・馮卡曼邊界條件的波函數出發，再搭配週期位能條件，得到布拉赫定理。如此的證明可讓我們更了解薛丁格方程的作用，以及究竟該如何求解波函數，就這意義上，第二種證明是更加基礎且重要的，但它的數學記號也難免較為複雜。

首先，對於所有滿足波恩・馮卡曼邊界條件的波函數，我們知道它一定能藉由“同樣滿足此邊界條件的波函數”所展開，並且其波向量 $\mathbf{q}$ 滿足 Eq.$(\ref{28})$。因此，

$$\psi(\mathbf{r})=\sum_{\mathbf{q}}c_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\tag{31}\label{31}$$

接著，由於位能 $U(\mathbf{r})$ 具有晶格常數的空間週期，所以它必然也能由同樣具有此週期的波函數所展開，因此，這些波函數也就有著等同於“倒晶格向量”的波向量：

$$U(\mathbf{r})=\sum_{\mathbf{K}}U_\mathbf{K}e^{i\mathbf{K}\cdot\mathbf{r}}\tag{32}\label{32}$$

此外，其傅立葉係數 $U_\mathbf{K}$ 與 $U(\mathbf{r})$ 的關係為：

$$U_\mathbf{K}=\frac{1}{v}\int_\text{cell}e^{i\mathbf{K}\cdot\mathbf{r}}U(\mathbf{r})d\mathbf{r}\tag{33}\label{33}$$

由於總是能對位能 $U(\mathbf{r})$ 加上任意常數，因此我們藉由“位能在一個原初晶格（primitive cell）內的空間平均為零”的要求來決定此常數：

$$U_0\equiv\frac{1}{v}\int_\text{cell}U(\mathbf{r})d\mathbf{r}=0\tag{34}\label{34}$$

值得注意的是，由於我們只考慮屬於實數的位能 $U(\mathbf{r})$，所以由 Eq.$(\ref{33})$ 可知，其傅立葉係數 $U_\mathbf{K}$ 滿足以下關係：

$$U_{-\mathbf{K}}=U_\mathbf{K}^*\tag{35}\label{35}$$

倘若我們進一步假設晶格具有反轉對稱性（inversion symmetry），也就是說，只要選擇適當的座標原點，就可使 $U(-\mathbf{r})=U(\mathbf{r})$ 成立，那麼 Eq.$(\ref{33})$ 蘊含了 $U_\mathbf{K}$ 亦為實數的結果，因此，

$$U_{-\mathbf{K}}=U_\mathbf{K}=U_\mathbf{K}^*\tag{36}\label{36}$$

話說回來，我們可將 Eq.$(\ref{31})$、Eq.$(\ref{32})$ 代入薛丁格方程式 Eq.$(\ref{2})$。其動能項為：

$$\frac{p^2}{2m}\psi=-\frac{\hbar^2}{2m}\nabla^2\psi=\sum_\mathbf{q}\frac{\hbar^2}{2m}q^2c_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\tag{37}\label{37}$$

並且其位能項為：

$$\begin{align*}U\psi&=\left(\sum_\mathbf{K}e^{i\mathbf{K}\cdot\mathbf{r}}\right)\left(\sum_\mathbf{q}c_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\right)\tag{38a}\label{38a}\\[5pt]&=\sum_{\mathbf{K}\mathbf{q}}U_\mathbf{K}c_\mathbf{q}e^{i(\mathbf{K}+\mathbf{q})\cdot\mathbf{r}}=\sum_{\mathbf{K}\mathbf{q}^\prime}U_\mathbf{K}c_{\mathbf{q}^\prime-\mathbf{K}}e^{i\mathbf{q}^\prime\cdot\mathbf{r}}\tag{38b}\label{38b}\end{align*}$$

接著，基於待會的方便，我們將 Eq.$(\ref{38b})$ 中的指標 $\mathbf{K}$、$\mathbf{q}^\prime$ 依序改為 $\mathbf{K}^\prime$ 與 $\mathbf{q}$，所以在考慮 Eq.$(\ref{37})$、Eq.$(\ref{38b})$ 之後，薛丁格方程式 Eq.$(\ref{2})$ 變為：

$$\begin{align*}-\frac{\hbar^2}{2m}\psi+U\psi&=\sum_\mathbf{q}\frac{\hbar^2}{2m}q^2c_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}+\sum_{\mathbf{K}^\prime \mathbf{q}}U_{\mathbf{K}^\prime}c_{\mathbf{q}-\mathbf{K}^\prime}e^{i\mathbf{q}\cdot\mathbf{r}}\tag{39a}\label{39a}\\[5pt]&=\sum_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\left(\frac{\hbar^2}{2m}q^2c_\mathbf{q}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime}c_{\mathbf{q}-\mathbf{K}^\prime}\right)\tag{39b}\label{39b}\\[5pt]&=\varepsilon\psi\tag{39c}\label{39c}\\[5pt]&=\varepsilon\sum_\mathbf{q}c_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\tag{39d}\label{39d}\end{align*}$$

也就是說，

$$\sum_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\left[\left(\frac{\hbar^2}{2m}q^2-\varepsilon\right)c_\mathbf{q}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime}c_{\mathbf{q}-\mathbf{K}^\prime}\right]=0\tag{40}\label{40}$$

由於滿足波恩・馮卡曼邊界條件的平面波 $e^{i\mathbf{q}\cdot\mathbf{r}}$ 是互相正交的，所以 Eq.$(\ref{40})$ 中的各項 $e^{i\mathbf{q}\cdot\mathbf{r}}$ 係數必然皆為零，因此，對於所有滿足 Eq.$(\ref{28})$ 的波向量 $\mathbf{q}$ 而言：

$$\left(\frac{\hbar^2}{2m}q^2-\varepsilon\right)c_\mathbf{q}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime}c_{\mathbf{q}-\mathbf{K}^\prime}=0\tag{41}\label{41}$$

根據 Eq.$(\ref{28})$，波向量 $\mathbf{q}$ 是由倒晶格向量的原初向量 $\mathbf{b}_i$ 所組成，其各項係數為 $1/N_i$ 之整數倍，所以波向量 $\mathbf{q}$ 不必然落於倒晶格點上（即整數倍的 $\mathbf{b}_i$ 的線性組合）。因此，我們總是能夠將波向量 $\mathbf{q}$ 改寫為 $\mathbf{k}-\mathbf{K}$，其中 $\mathbf{K}$ 是倒晶格向量（$\mathbf{K}=\sum_i n_i\mathbf{b}_i$，$n_i\in\mathbb{N}$），使得 $\mathbf{k}$ 恰好都落於第一布里淵區（first Brillouin zone）內。因此，Eq.$(\ref{41})$ 變為：

$$\left(\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}\right\vert^2-\varepsilon\right)c_{\mathbf{k}-\mathbf{K}}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime}c_{\mathbf{k}-\mathbf{K}-\mathbf{K}^\prime}=0\tag{42}\label{42}$$

最後，我們再做一個變數代換，將所有 $\mathbf{K}^\prime$ 指標平移 $\mathbf{K}$，即 $\mathbf{K}^\prime\to\mathbf{K}^\prime-\mathbf{K}$。由於 Eq.$(\ref{42})$ 是對於任一特定波向量 $\mathbf{q}$ 而言，所以倒晶格向量 $\mathbf{K}$ 對於 Eq.$(\ref{42})$ 中的 $\sum_{\mathbf{K}^\prime}$ 而言僅僅是個常數向量。如此一來，我們就能將薛丁格方程式 Eq.$(\ref{2})$ 改寫為以倒晶格向量（晶格動量）為基礎的形式：

$$\left(\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}\right\vert^2-\varepsilon\right)c_{\mathbf{k}-\mathbf{K}}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime-\mathbf{K}}c_{\mathbf{k}-\mathbf{K}^\prime}=0\tag{43}\label{43}$$

之所以能有如此這般的形式，是由於週期位能使得只有當 $\mathbf{K}$ 為倒晶格向量時（reciprocal lattice vector），$U_\mathbf{K}$ 才不為零。

由於有無窮個滿足 Eq.$(\ref{28})$ 且總是能藉由適當的 $\mathbf{K}$ 平移至第一布里淵區中的特定 $\mathbf{k}$ 的 $\mathbf{q}$ ，所以對於任何一個落於第一布里淵區的 $\mathbf{k}$ 而言，它有無窮個 Eq.$(\ref{43})$，而這無窮多條方程式就構成「一組」方程組，可用來解出特定 $\mathbf{k}$ 的各項係數 $c_{\mathbf{k}-\mathbf{K}}$、$c_{\mathbf{k}-\mathbf{K}^\prime}$、$c_{\mathbf{k}-\mathbf{K}^{\prime\prime}}$、⋯⋯，這些波向量都與 $\mathbf{k}$ 差一個倒晶格向量（reciprocal lattice vector）。

而由於每個布里淵區都只能容納 $N$ 個波向量（見 Eq.$(\ref{29})$），所以我們就能將原本的薛丁格方程式改寫為 $N$ 組聯立方程式的數學問題；每一組聯立方程式都是只針對落於第一布里淵區的一個 $\mathbf{k}$，其所求出的 $\varepsilon$（特徵值）也就是與 $\mathbf{k}$ 有關的函數，即 $\varepsilon_\mathbf{k}(\mathbf{r})$。

$$\begin{align*}&\left\{\begin{aligned}\left(\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_1\right\vert^2-\varepsilon_\mathbf{k}\right)c_{\mathbf{k}-\mathbf{K}_1}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime-\mathbf{K}_1}c_{\mathbf{k}-\mathbf{K}^\prime}&=0\\[5pt]\left(\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_2\right\vert^2-\varepsilon_\mathbf{k}\right)c_{\mathbf{k}-\mathbf{K}_2}+\sum_{\mathbf{K}^\prime}U_{\mathbf{K}^\prime-\mathbf{K}_2}c_{\mathbf{k}-\mathbf{K}^\prime}&=0\\[5pt]\cdots&=0\\[5pt]\cdots&=0\end{aligned}\right.\tag{44a}\label{44a}\\[5pt]\implies&\begin{pmatrix}\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_1\right\vert^2-\varepsilon_\mathbf{k}+U_0&U_{\mathbf{K}_2-\mathbf{K}_1}&\cdots\\[5pt]U_{\mathbf{K}_1-\mathbf{K}_2}&\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_2\right\vert^2-\varepsilon_\mathbf{k}+U_0&\cdots\\[5pt]\cdots&\cdots&\cdots\end{pmatrix}\begin{pmatrix}c_{\mathbf{k}-\mathbf{K}_1}\\[5pt]c_{\mathbf{k}-\mathbf{K}_2}\\[5pt]\vdots\end{pmatrix}=\begin{pmatrix}0\\[5pt]0\\[5pt]\vdots\end{pmatrix}\tag{44b}\label{44b}\\[5pt]\implies&\begin{pmatrix}\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_1\right\vert^2-\varepsilon_\mathbf{k}&U_{\mathbf{K}_2-\mathbf{K}_1}&\cdots\\[5pt]U_{\mathbf{K}_1-\mathbf{K}_2}&\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_2\right\vert^2-\varepsilon_\mathbf{k}&\cdots\\[5pt]\cdots&\cdots&\cdots\end{pmatrix}\begin{pmatrix}c_{\mathbf{k}-\mathbf{K}_1}\\[5pt]c_{\mathbf{k}-\mathbf{K}_2}\\[5pt]\vdots\end{pmatrix}=\begin{pmatrix}0\\[5pt]0\\[5pt]\vdots\end{pmatrix}\tag{44c}\label{44c}\end{align*}$$

在上述矩陣中，$\mathbf{K}_i=\sum_j n_j\mathbf{b}_j$ 且 $n_j\in\mathbb{N}$，並且已代入 Eq.$(\ref{34})$ 的 $U_0=0$ 條件。由此可見，每一組聯立方程式的解 $c_{\mathbf{k}-\mathbf{K}}$，都只有 $\mathbf{k}$ 這個波向量以及與其相差一個倒晶格向量的波向量的波：

$$\begin{align*}\psi(\mathbf{r})&=\sum_\mathbf{q}c_\mathbf{q}e^{i\mathbf{q}\cdot\mathbf{r}}\tag{45a}\label{45a}\\[5pt]&=\sum_{\mathbf{k}\in\text{1st B.Z.}}\psi_\mathbf{k}(\mathbf{r})\tag{45b}\label{45b}\\[5pt]&=\sum_{\mathbf{k}\in\text{1st B.Z.}}\sum_\mathbf{K}c_{\mathbf{k}-\mathbf{K}}e^{i(\mathbf{k}-\mathbf{K})\cdot\mathbf{r}}\tag{45c}\label{45c}\end{align*}$$

進一步觀察 $\psi_\mathbf{k}(\mathbf{r})$，可發現：

$$\begin{align*}\psi_k(\mathbf{r})&=e^{i\mathbf{k}\cdot\mathbf{r}}\left(\sum_{\mathbf{K}}c_{\mathbf{k}-\mathbf{K}}e^{-i\mathbf{K}\cdot\mathbf{r}}\right)\tag{46a}\label{46a}\\[5pt]&=e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})\tag{46b}\label{46b}\end{align*}$$

其中，$u_\mathbf{k}(\mathbf{r})\equiv\sum_{\mathbf{K}}c_{\mathbf{k}-\mathbf{K}}e^{-i\mathbf{K}\cdot\mathbf{r}}$，並且滿足底下的週期條件：

$$u_\mathbf{k}(\mathbf{r}+\mathbf{R})=u_\mathbf{k}(\mathbf{r})\tag{47}\label{47}$$

也就是布拉赫定理。

布拉赫定理的物理內涵

一、晶格動量 $\hbar\mathbf{k}$

雖然這裡引入的波向量 $\mathbf{k}$ 與索末菲（Sommerfeld）自由電子模型（free electron model）中的波向量 $\mathbf{k}$ 看似是差不多的，但其實並不同。因為自由電子模型中的 $\mathbf{k}$ 確實等於 $\mathbf{p}/\hbar$，然而這裡的 $\mathbf{k}$ 並沒有此關係；因為目前考慮的位能並沒有平移對稱性，所以布拉赫定理中的波向量 $\mathbf{k}$ 與電子動量沒有直接關係。

也就是說，Hamiltonian 的特徵態並非同時是動量算符 $\mathbf{p}=(\hbar/i)\nabla$ 的特徵態。具體來說，倘若我們將 $\mathbf{p}$ 作用於 $\psi_\mathbf{k}$ 上：

$$\begin{align*}\frac{\hbar}{i}\nabla\psi_\mathbf{k}&=\frac{\hbar}{i}\nabla\left[e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})\right]\tag{48a}\label{48a}\\[5pt]&=\hbar\mathbf{k}\psi_\mathbf{k}+e^{i\mathbf{k}\cdot\mathbf{r}}\frac{\hbar}{i}\nabla u_\mathbf{k}(\mathbf{r})\tag{48b}\label{48b}\end{align*}$$

會發現仍然留有不與 $\psi_\mathbf{k}$ 成比例的第二項。然而，倘若我們的位能 $U(r)$ 是獨立於位置座標的常數，即 Eq.$(\ref{32})$ 可簡化為 $U(r)=U_0=0$，那麼 Eq.$(\ref{44c})$ 就可簡化為：

$$\begin{pmatrix}\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_1\right\vert^2-\varepsilon_\mathbf{k}&0&\cdots\\[5pt]0&\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_2\right\vert^2-\varepsilon_\mathbf{k}&\cdots\\[5pt]\cdots&\cdots&\cdots\end{pmatrix}\begin{pmatrix}c_{\mathbf{k}-\mathbf{K}_1}\\[5pt]c_{\mathbf{k}-\mathbf{K}_2}\\[5pt]\vdots\end{pmatrix}=\begin{pmatrix}0\\[5pt]0\\[5pt]\vdots\end{pmatrix}\tag{49}\label{49}$$

此時，若要有解，那麼必然是：

$$\left\{\begin{aligned}\varepsilon_\mathbf{k}&=\frac{\hbar^2}{2m}\left\vert\mathbf{k}-\mathbf{K}_i\right\vert^2,\quad c_{\mathbf{k}-\mathbf{K}_j}=0,\quad \forall j\neq i\\[5pt]\psi_\mathbf{k}&=c_{\mathbf{k}-\mathbf{K}_i}e^{i(\mathbf{k}-\mathbf{K}_i)\cdot\mathbf{r}}\end{aligned}\right.\tag{50}\label{50}$$

也就是說，先前的 $u_\mathbf{k}(\mathbf{r})$ 變為：

$$\begin{align*}u_\mathbf{k}(\mathbf{r})&=\sum_\mathbf{K}c_{\mathbf{k}-\mathbf{K}}e^{-i\mathbf{K}\cdot\mathbf{r}}\tag{51a}\label{51a}\\[5pt]&=c_{\mathbf{k}-\mathbf{K}_i}e^{-i\mathbf{K}_i\cdot\mathbf{r}}\tag{51b}\label{51b}\end{align*}$$

最後，將 Eq.$(\ref{51b})$ 代入 Eq.$(\ref{48b})$，我們就會發現此時的 $\psi_\mathbf{k}$ 既是 Hamiltonian 的特徵態，也是動量算符 $\mathbf{p}$ 的特徵態。

$$\begin{align*}\mathbf{p}\psi_\mathbf{k}&=\hbar\mathbf{k}\psi_\mathbf{k}+e^{i\mathbf{k}\cdot\mathbf{r}}\frac{\hbar}{i}\nabla u_\mathbf{k}(\mathbf{r})\tag{52a}\label{52a}\\[5pt]&=\hbar\mathbf{k}\psi_\mathbf{k}-\hbar\mathbf{K}_i\underbrace{c_{\mathbf{k}-\mathbf{K}_i}e^{i(\mathbf{k}-\mathbf{K}_i)\cdot\mathbf{r}}}_{\psi_\mathbf{k}}\tag{52b}\label{52b}\\[5pt]&=\hbar\left(\mathbf{k}-\mathbf{K}_i\right)\psi_\mathbf{k}\tag{52c}\label{52c}\end{align*}$$

總而言之，只有當位能 $U(r)$ 獨立於位置、具有空間平移對稱性時，我們才能將波向量 $\mathbf{k}$ 詮釋為與速度正比的動量 $\mathbf{p}$ 有關的物理量。

然而，由於 $\hbar\mathbf{k}$ 實在是很像動量 $\mathbf{p}$，並且也由於布拉赫電子（Bloch electron）在電磁場中的運動方程式，使得我們仍然將 $\hbar\mathbf{k}$，或是 $\mathbf{k}$，稱之為晶格動量（Crystal momentum），即便在週期位能下，$\hbar\mathbf{k}$ 真的不是電子的動量。布拉赫電子在電磁場中的運動方程式為：

$$\begin{align*}\dot{\mathbf{r}}&\equiv\mathbf{v}_n(\mathbf{k})=\frac{1}{\hbar}\frac{\partial\varepsilon_n(\mathbf{k})}{\partial \mathbf{k}}\tag{53a}\label{53a}\\[5pt]\hbar\dot{\mathbf{k}}&=-e\left[\mathbf{E}(\mathbf{r},t)+\frac{1}{c}\mathbf{v}_n(\mathbf{k})\times\mathbf{H}(\mathbf{r},t)\right]\tag{53b}\label{53b}\end{align*}$$

其中的 $1/c$ 請詳見高斯單位制。單看 Eq.$(\ref{53b})$，會讓人情不自禁覺得 $\hbar\mathbf{k}$ 當然就是動量了！然而，Eq.$(\ref{53b})$ 中其實並沒有晶格週期位能 $U(r)$，式中的 $\mathbf{E}(\mathbf{r})$ 是外加電場，而非內在的晶格電場。那麼晶格週期位能 $U(r)$ 跑到哪去了呢？其實它被併到 Eq.$(\ref{53a})$ 中的速度 $\mathbf{v}_n(\mathbf{k})$ 中了！換言之，Eq.$(\ref{53b})$ 並不是古典力學意義上的 $\mathbf{F}_\text{net}=m\mathbf{a}$，它只是“長得很像”。因此，基於這組電子動力學的半古典模型（Semiclassical model of electron dynamics），我們特別喜歡將 $\hbar\mathbf{k}$ 稱為晶格動量。

二、布拉赫波向量 $\mathbf{k}$ “能夠”總是處於第一布里淵區中

雖然布拉赫定理本身並沒有限制波向量 $\mathbf{k}$ 的範圍，即便搭配了波恩・馮卡曼邊界條件，那也只是多了 Eq.$(\ref{28})$ 的限制，但我們總是能夠將任何不處於第一布里淵區的 $\mathbf{k}^\prime$，改寫為 $\mathbf{k}^\prime=\mathbf{k}+\mathbf{K}$，其中 $\mathbf{k}\in\text{1st. B.Z.}$ 並且 $\mathbf{K}$ 為倒晶格向量（$\mathbf{b}_i$ 之整數線性組合），使得 $e^{i\mathbf{K}\cdot\mathbf{R}}=1$。從布拉赫定理的第一種證明 Eq.$(\ref{21})$ 就能看清楚此關係：

$$\begin{align*}\psi(\mathbf{r}+\mathbf{R})&=e^{i\mathbf{k}^\prime\cdot\mathbf{R}}\psi(\mathbf{r})\tag{54a}\label{54a}\\[5pt]&=e^{i(\mathbf{k}+\mathbf{K})\cdot\mathbf{R}}\psi(\mathbf{r})\tag{54b}\label{54b}\\[5pt]&=e^{i\mathbf{k}\cdot\mathbf{R}}\psi(\mathbf{r})\tag{54c}\label{54c}\end{align*}$$

至於第二種證明則不必多說，因為它早已將最後波函數中的波向量 $\mathbf{k}$ 改寫至第一布里淵區中了。也就是說，只要 $\mathbf{k}^\prime$ 滿足布拉赫定理，那麼滿足 $\mathbf{k}^\prime=\mathbf{k}+\mathbf{K}$ 的第一布里淵區中的波向量 $\mathbf{k}$ 也就必然滿足。第一與第二種證明使得我們總是在布拉赫電子波函數的下標給上一個落於第一布里淵區中的 $\mathbf{k}$，即

$$\psi(\mathbf{r})=\psi_\mathbf{k}(\mathbf{r})\tag{55}\label{55}$$

三、$\varepsilon_{n\mathbf{k}}$、$\varepsilon_n(\mathbf{k})$、$\psi_{n\mathbf{k}}$ 中的 $n$ 的意義？

由第二種證明中的 Eq.$(\ref{44c})$ 可以看到，對於任何特定 $\mathbf{k}$，都存在著無窮個 $\varepsilon_\mathbf{k}$，使得薛丁格方程式成立。也就是說，在倒晶格 $\mathbf{k}$ 空間中，每個離散的 $\mathbf{k}$ 上，都存有著無窮個可能的能量特徵態。因此，我們說這是 $\mathbf{k}$ 上的“能階”，並標記為 $\varepsilon_{n\mathbf{k}}$。

我們也可直接將布拉赫波函數 $\psi_\mathbf{k}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})$ 直接代入薛丁格方程式 Eq.$(\ref{2})$ 中：

$$\begin{align*}H\psi_\mathbf{k}(\mathbf{r})&=\left[-\frac{\hbar^2}{2m}\nabla^2+U(\mathbf{r})\right]\psi_\mathbf{k}(\mathbf{r})\tag{56a}\label{56a}\\[5pt]&=-\frac{\hbar^2}{2m}\nabla^2\left[e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})\right]+U(\mathbf{r})e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})\tag{56b}\label{56b}\\[5pt]&=-\frac{\hbar^2}{2m}\nabla\left[i\mathbf{k}e^{i\mathbf{k}\cdot\mathbf{r}} u_\mathbf{k}(\mathbf{r})+e^{i\mathbf{k}\cdot\mathbf{r}}\nabla u_\mathbf{k}(\mathbf{r})\right]+U(\mathbf{r})e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})\tag{56c}\label{56c}\\[5pt]&=-\frac{\hbar^2}{2m}\left[i^2\vert\mathbf{k}\vert^2e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})+2i\mathbf{k}e^{i\mathbf{k}\cdot\mathbf{r}}\nabla u_\mathbf{k}(\mathbf{r})+e^{i\mathbf{k}\cdot\mathbf{r}}\nabla^2u_\mathbf{k}(\mathbf{r})\right]+U(\mathbf{r})e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})\tag{56d}\label{56d}\\[5pt]&=e^{i\mathbf{k}\cdot\mathbf{r}}\left[\frac{\hbar^2}{2m}\frac{1}{i^2}\left(i^2\vert\mathbf{k}\vert^2+2i\mathbf{k}\nabla+\nabla^2\right)u_\mathbf{k}(\mathbf{r})+U(\mathbf{r})u_\mathbf{k}(\mathbf{r})\right]\tag{56e}\label{56e}\\[5pt]&=e^{i\mathbf{k}\cdot\mathbf{r}}\left[\frac{\hbar^2}{2m}\frac{1}{i^2}\left(i\mathbf{k}+\nabla\right)^2+U(\mathbf{r})\right]u_\mathbf{k}(\mathbf{r})\tag{56f}\label{56f}\\[5pt]&=e^{i\mathbf{k}\cdot\mathbf{r}}\left[\frac{\hbar^2}{2m}\left(\frac{1}{i}\nabla+\mathbf{k}\right)^2+U(\mathbf{r})\right]u_\mathbf{k}(\mathbf{r})\tag{56g}\label{56g}\\[5pt]&=\varepsilon_\mathbf{k}\underbrace{e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r})}_{\psi_\mathbf{k}(\mathbf{r})}\tag{56h}\label{56h}\end{align*}$$

從 Eq.$(\ref{56g})$、Eq.$(\ref{56h})$，將 $e^{i\mathbf{k}\cdot\mathbf{r}}$ 消去後，可以看到特徵值偏微分方程式：

$$\left[\frac{\hbar^2}{2m}\left(\frac{1}{i}\nabla+\mathbf{k}\right)^2+U(\mathbf{r})\right]u_\mathbf{k}(\mathbf{r})=\varepsilon_\mathbf{k} u_\mathbf{k}(\mathbf{r})\tag{57}\label{57}$$

並搭配著底下的週期性邊界條件（源自週期位能）：

$$u_\mathbf{k}(\mathbf{r}+\mathbf{R})=u_\mathbf{k}(\mathbf{r})\tag{58}\label{58}$$

根據 Sturm-Liouville theory，這是一種被限縮於原初晶格範圍內的 Hermitian 特徵值問題（Hermitian eigenvalue problem），因此它有無窮個離散的特徵值，並且我們用 $n$ 來標記它們。此外，就以 Eq.$(\ref{57})$、Eq.$(\ref{58})$ 而言，波向量 $\mathbf{k}$ 其實只是一個“參數”，所以說，我們預期當波向量 $\mathbf{k}$ “連續變化”時，特定 $n$ 的能階 $\varepsilon_{n\mathbf{k}}$ 也會隨著“連續變化”。因此，就這意義上，我們又將能階 $\varepsilon_{n\mathbf{k}}$ 改寫為 $\varepsilon_n(\mathbf{k})$。也因此，我們說電子在週期位能下的能階，是由無窮個在倒晶格 $\mathbf{k}$ 空間上連續的 $\varepsilon_n(\mathbf{k})$ 函數所組成的。

四、其他布里淵區呢？

剛才我們提到，第一種證明只有 Eq.$(\ref{28})$ 的波向量要求，所以不論 $\mathbf{k}$ 落於第幾布里淵區，布拉赫定理都成立。換言之，處於晶格週期位能下的布拉赫電子，可以擁有各種布里淵區內的波向量 $\mathbf{k}$。而在第二種證明，雖然我們由 Eq.$(\ref{41})$ 至 Eq.$(\ref{42})$ 的推論中做了 $\mathbf{q}=\mathbf{k}-\mathbf{K}$ 的平移，使得 $\mathbf{k}$ 落於第一布里淵區中，但其實就算平移到第二、第三布里淵區，其結果 Eq.$(\ref{42})$、Eq.$(\ref{43})$ 也是相同的！由 Eq.$(\ref{44c})$ 可以看到，其能階分佈 $\varepsilon_n(\mathbf{k})$ 並不會受到 $\mathbf{k}$ 是落在第幾個布里淵區的影響而改變，畢竟總是有 $\mathbf{K}_i$ 抵銷、平移它，使其結果最後都對稱於第一布里淵區的 $\mathbf{k}$ 值結果。

也就是說，以能階 $\varepsilon_n(\mathbf{k})$ 的角度而言，對於任何一個 $n$，特徵值 $\varepsilon_n(\mathbf{k})$ 與特徵態 $\psi_{n,\mathbf{k}}(\mathbf{r})$ 都是在倒（晶格）空間（$\mathbf{k}$ 空間）中的週期函數，並以倒晶格向量 $\mathbf{K}$ 為週期：

$$\begin{align*}\psi_{n,\mathbf{k}+\mathbf{K}}(\mathbf{r})&=\psi_{n,\mathbf{k}}(\mathbf{r})\tag{59a}\label{59a}\\[5pt]\varepsilon_{n}(\mathbf{k}+\mathbf{K})&=\varepsilon_n(\mathbf{k})\tag{59b}\label{59b}\end{align*}$$

因此，我們將這種“對於每個 $n$ 而言，在倒空間中的能量週期結構”稱之為“能帶結構”（Energy band structure）。每個 $n$ 的 $\varepsilon_n(\mathbf{k})$，都是一條（一片？）能帶。

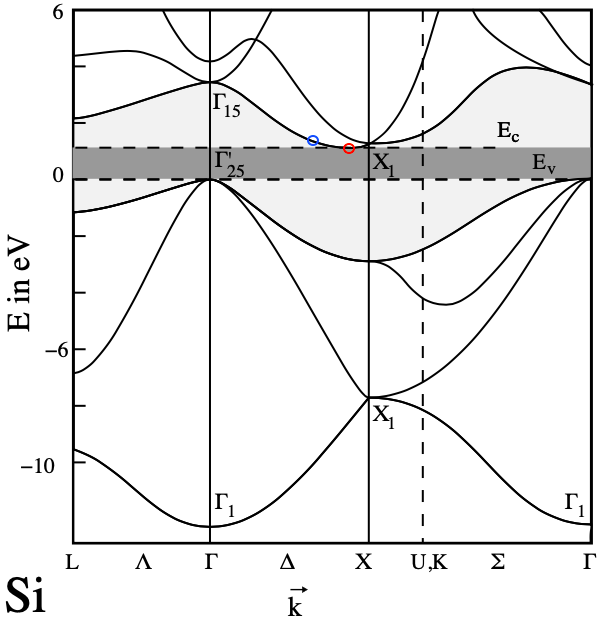
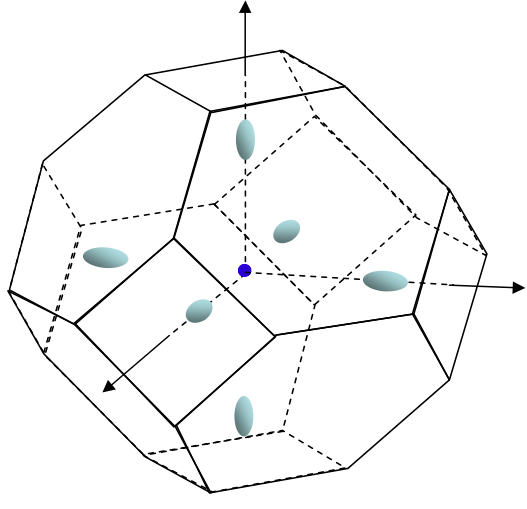
圖一中的三軸就是 $k_x$、$k_y$ 與 $k_z$，外圍的稜角邊界就是第一布里淵區的範圍。而圖中六個橢球“面”就是能量恰好等於矽的傳導帶（conduction band）的所有 $\mathbf{k}$ 值構成的表面。也就是滿足 $\varepsilon_n(\mathbf{k})=\varepsilon_c + \delta\varepsilon$ 的所有 $\mathbf{k}$ 值。其中 $d\varepsilon$ 是指，這種圖一定不是指 $\varepsilon_n(\mathbf{k})=\varepsilon_c$，因為若是如此，那不會是六個橢球，而會是六個“點”，所以肯定是在傳導帶“附近”，因此我將那附近的“差值”以 $d\varepsilon$ 表示。

圖二中的紅圈就是 $\varepsilon_n(\mathbf{k})=\varepsilon_c$ 的位置，而我所說的“ $\varepsilon_c$ 附近” 就是指如藍圈的位置。將能量等同於藍圈的所有 $\mathbf{k}$ 描繪出來，在 $\mathbf{k}$ 空間上才會是六顆橢球面（不是實心橢球）。

五、電子速度

倘若波向量為 $\mathbf{k}$ 的電子始終處在特定能帶 $n$ 上的話，我們可以證明其速度不僅不為零（請參考 Ashcroft & Mermin Appendix E (1976)），而且還會是

$$\mathbf{v}_n=\frac{1}{\hbar}\nabla_\mathbf{k}\varepsilon_n(\mathbf{k})\tag{60}\label{60}$$

這代表了什麼呢？這表示，在理想週期位能中的電子，並不像是我們在國高中對金屬電子的想像（即 Drude model），在各顆原子之間碰來撞去、彈來飛去。反之，即便沒有施加電場，電子的運動也是相當規律，它必然與其既定的能帶結構有 Eq.$(\ref{60})$ 的關係，而且不會越撞越慢。

總結

晶格週期位能使得晶格裡的電子（Hamiltonian 的特徵態 $\varepsilon_{n,\mathbf{k}}(\mathbf{r})$ 只能有著離散且滿足 Eq.$(\ref{28})$ 的波向量，它們之間的最小間隔 $\Delta\mathbf{k}$ 恰好是平均每個原子在任意布里淵區中能分配到的體積，即 $(2\pi)^3/V$。所謂的晶格動量其實是基於布拉赫電子運動方程式所與牛頓力學類比所得到的概念，除非週期位能不隨位置改變，否則 $\hbar\mathbf{k}$ 並非布拉赫電子 $\psi_{n,\mathbf{k}}(\mathbf{r})$ 的動量。因為晶格的週期性，所以能藉邊界條件將薛丁格方程式化約為僅限縮在原初晶胞（primitive cell）裡的 Hermitian 特徵值問題，使其具有無窮多個特徵值 $\varepsilon_\mathbf{k}$，也就構成 $\varepsilon_{n,\mathbf{k}}$，並在數學上對於 $\mathbf{k}$ 為連續函數，即可寫為 $\varepsilon_n(\mathbf{k})$。最後，因為位能具有晶格常數的週期，所以特徵態 $\psi_{n,\mathbf{k}}$ 與特徵值 $\varepsilon_n(\mathbf{k})$ 在倒空間中必然有著倒晶格向量 $\mathbf{K}$ 的週期，使得對於每個 $n$ 而言，產生了所謂的“能帶結構”。

簡單來說，這一切都是來自週期位能。

---

也許你也有興趣閱讀：

• 〈給一點找指導教授的建議〉
• 〈半導體元件物理學習書單與心得〉
• 〈Sentaurus TCAD 筆記〉
• 〈雪崩光偵測器之崩潰電壓 Python 模擬器〉
• 〈布拉格與勞厄繞射之等價證明〉
• 〈什麼是 Density of states？〉
• 〈本質半導體的載子濃度推導〉

---