在常見的 Neaman 固態電子學教科書中,電子濃度($n\equiv N/V$)的推導是藉由自由電子氣體模型的能階密度所類比得到的。我希望能在這篇文章,由半古典電子動力學模型、能帶理論、倒空間、費米面等觀念,大致完整走過一次物理推導。以求在「不使用類比」的前提下,由物理的方法得到所謂的電子載子濃度:
$$n=\int_{\varepsilon_c}^{\infty}g_c(\varepsilon)f(\varepsilon)d\varepsilon$$
其中,$g_c(\varepsilon)$ 為在能階能量為 $\varepsilon$ 時,能階數目隨著能量 $\varepsilon$ 改變的變化速率。根據採用的普朗克常數,有兩種不同寫法:
$$g_c(\varepsilon)=\frac{4\pi(2m_c)^{3/2}}{h^3}\sqrt{\varepsilon-\varepsilon_c}=\frac{m_c^{3/2}}{\pi^2\hbar^3}\sqrt{2(\varepsilon-\varepsilon_c)}$$
所謂的自由電子模型,是指在完全忽略電子間交互作用,並且讓這些電子在完全沒有位能的情況下,所推得的波函數組態。這一直讓我很困擾,畢竟實際上半導體中的傳導電子並不是處在一個完全沒有位能的環境中。這些傳導電子——或者說價電子——其實是位於具有著週期性的位能環境中,從而使得布拉赫理論(Bloch theorem)成立。
$$\left[-\frac{\hbar^2}{2m}\nabla^2+U(\mathbf{r})\right]\psi=\varepsilon\psi$$
$$U(\mathbf{r})=U(\mathbf{r}+\mathbf{R})\quad\to\quad\psi(\mathbf{r}+\mathbf{R})=e^{i\mathbf{k}\cdot\mathbf{R}}\psi(\mathbf{r})$$
其中,$\mathbf{R}$ 為布拉菲晶格(Bravais lattice)中的任意晶格向量 $\mathbf{R}\equiv n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\;,\;n_i\in\mathbb{Z}$。並且 $\mathbf{k}$ 為倒晶格(reciprocal lattice)中的任意向量:$\mathbf{k}=x_1\mathbf{b}_1+x_2\mathbf{b}_2+x_3\mathbf{b}_3\;,\;x_i\in\mathbb{C}$。而在搭配玻恩—卡曼邊界條件(Born-Von Karman boundary condition)後,我們可得到波向量 $\mathbf{k}$ 中的 $x_i$ 為 $x_i=m_i/N_i$ 的實數且 $m_i$ 為整數的解($N_i$ 為布拉菲晶格在 $\mathbf{a}_i$ 方向上的基本晶胞(primitive cell)數目,$N_i\equiv L/a_i$)。
這是我第一篇使用固態物理以試圖解釋常見半導體物理公式的文章。除了想寫給同樣有興趣了解的讀者以外,也是想試著用自己的話、熟悉的中文語言,重新解釋清楚究竟我學了什麼。由於我的固態物理是自學的,所以可能有些錯誤,還請多多包涵。
我不知道有沒有人跟我一樣,對於工程的東西,就是比較難直接吞下去,總是希望可以由物理學、第一原理盡可能地推下去。相信你應該會覺得這根本瘋了,但我也不知道為什麼,我自己大概只有這樣才能把那些工程學科學得好。這也是為什麼我的固態電子學總是學得很吃力,因為很難(在感情上?)接受那些觀念、推論。對我而言,那些類比的說服力並不足夠強,我希望能看到更多的物理上的詳細推導,我才能夠在心中有所謂的物理直覺、圖像等。這篇文章,我想談談應該算是第一個重要的半導體物理公式。這篇文章用到很多我沒有細講的概念,一方面是自己也不清楚背後的深厚理論,二方面是即便清楚,也沒有足夠時間寫文章交待清楚。但如果你想知道更多某部分的物理,是很歡迎你留言跟我說的。未來我也會找時間寫寫我覺得很基本且重要的固態物理觀念。
根據布拉赫定理以及玻恩—卡曼邊界條件,我們得到滿足具有週期位能之薛丁格方程式的特徵解為,有兩個量子數($n$ 與 $\mathbf{k}$)的布拉赫波函數(Bloch wave function):
$$\psi_{n\mathbf{k}}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_{n\mathbf{k}}(\mathbf{r})\tag{1}$$
而這兩個量子數的條件為:
$$n=1,2,3,\cdots\tag{2a}$$
$$\mathbf{k}=x_1\mathbf{b}_1+x_2\mathbf{b}_2+x_3\mathbf{b}_3,\quad x_i=\frac{m_i}{N_i}\tag{2b}$$
其中,$m_i\in\mathbb{Z}$。這個波函數的能量即為 $n$ 與 $\mathbf{k}$ 的函數:$\varepsilon=\varepsilon_n(\mathbf{k})$。而由於任何一個塊材都有著極多的基本晶胞,使得允許的 $\mathbf{k}$ 量子數間隔十分小,所以我們可姑且將 $\varepsilon_n({\mathbf{k}})$ 視為一個在 $\mathbf{k}$ 空間上連續的函數。如果在 $\mathbf{k}$ 空間中,任選一條線段,並畫出特定 $n$ 值沿著這軸的能量,那麼會觀察到連續蜿蜒的帶狀曲線(如圖一)。
因此,我們將量子數 $n$ 稱為能帶的量子數(band index)。因此,在這樣的量子系統中,電子的波函數即為這些特徵解的線性組合:
$$\psi(\mathbf{r},t)=\sum_{n’}\sum_{\mathbf{k}’}C_{n’,\mathbf{k}’}\psi_{n’\mathbf{k}’}(\mathbf{r})\;\text{exp}\left[-\frac{i}{\hbar}\varepsilon_{n}(\mathbf{k}’)t\right]\tag{3}$$
而根據 Ashcroft & Mermin 於 Solid State Physics 第 12 章所言,當外加電磁場的波長遠大於晶格常數,並且其振幅滿足下列條件而足夠小時:
$$eEa\ll\frac{[\varepsilon_{\text{gap}}(\mathbf{k})]^2}{\varepsilon_{\text{F}}}\tag{4a}$$
$$\hbar\omega_c\ll\frac{[\varepsilon_{\text{gap}}(\mathbf{k})]^2}{\varepsilon_{\text{F}}}\tag{4b}$$
此時,所謂的半古典電子動力學模型(Semiclassical Model of Electron Dynamics)就會成立。
半古典電子動力學模型
一、每個價電子都會佔據一個能帶 $n$ 以及一個波向量 $\mathbf{k}$,而每個電子的波包函數為:
$$\psi(\mathbf{r},t)\to\psi_n(\mathbf{r},t)=\sum_{\mathbf{k}’}C_{n,\mathbf{k}’}\psi_{n\mathbf{k}’}(\mathbf{r})\;\text{exp}\left[-\frac{i}{\hbar}\varepsilon_n(\mathbf{k})t\right]\tag{5}$$
其中,所謂的「每個電子都有一個波向量」的具體意義是,當 $\vert\mathbf{k}’-\mathbf{k}\vert>\Delta k$ 時,$ C_{n,\mathbf{k}’}\approx 0$。因此,$\Delta k$ 是這個波包的寬度。
二、該電子的速度——或說波包的群速度——為:
$$\mathbf{v}_n(\mathbf{k})=\frac{1}{\hbar}\frac{\partial\varepsilon_n(\mathbf{k})}{\partial\mathbf{k}}\tag{6}$$
三、電子的波向量滿足著與牛頓定律十分相似的方程式:
$$\hbar\dot{\mathbf{k}}=-e\left[\mathbf{E}(\mathbf{r},t)+\frac{1}{c}\mathbf{v}_n(\mathbf{k})\times\mathbf{H}(\mathbf{r},t)\right]\tag{7}$$
四、在每單位塊材體積中,每個 $(n,\mathbf{k})$ 數對都對應著兩個能階,分別對應兩方向的自旋。而在布拉菲第一區中,只要 $n$、$\mathbf{k}$ 有一者不同,那就是不同的數對。而平均每組 $(n,\mathbf{k})$ 數對對於電子濃度 $n$ 貢獻的電子數目期望值為(因為有考慮自旋,所以每組 $(n,\mathbf{k})$ 數對最多有兩個電子,但其機率不為 $1$。)
$$2\times f(\varepsilon_n(\mathbf{k}))\times\frac{1}{V}=f(\varepsilon_n(\mathbf{k}))\frac{\Delta\mathbf{k}}{4\pi^3}=\frac{\Delta\mathbf{k}/4\pi^3}{e^{(\varepsilon_n(\mathbf{k})-\mu)/k_BT}+1}\tag{8}$$
其中,$f(\varepsilon_n(\mathbf{k}))$ 為每組數對 $(n,\mathbf{k})$ 擁有的電子數目期望值。
基於第四點,我們可知能量越小的能階 $(n,\mathbf{k})$,其電子數越多。假如我們討論在 $T\to 0\left.\mathrm{K}\right.$ 的情形,那麼可以說,當能階的能量小於化學勢 $\mu$(chemical potential)時,每個能階的電子數期望值趨於 1,亦即每組 $(n,\mathbf{k})$ 數對上具有兩個電子(上下自旋)。由於每個布拉菲區都有著 $N=N_1N_2N_3$ 個波向量,而 $N$ 值又是這塊材所擁有的基本晶胞數目,而每個基本晶胞又只有一個原子。因此,在每個能帶中,都能夠存放與兩倍原子數的電子數(即 $2N$)。因此,假如所有的能帶,要嘛全部填滿,要嘛全部是空的,那麼該元素必然有著偶數個價電子。而對於全部被填滿的能帶而言,這能帶貢獻的電流密度必為零(這需要點數學證明,Ashcroft & Mermin Solid State Physics 的附錄 I 有它的數學證明):
$$\begin{align}j_n&=\lim_{V\to\infty}\sum_{\mathbf{k}}\frac{\Delta\mathbf{k}}{4\pi^3}f(\varepsilon_n(\mathbf{k}))\left(\frac{1}{\hbar}\frac{\partial \varepsilon_n(\mathbf{k})}{\partial \mathbf{k}}\right)\tag{9a}\\[4ex]&=(-e)\int_{C}\frac{d\mathbf{k}}{4\pi^3}f(\varepsilon_n(\mathbf{k}))\left(\frac{1}{\hbar}\frac{\partial \varepsilon_n(\mathbf{k})}{\partial \mathbf{k}}\right)\tag{9b}\\[4ex]&=0\tag{9c}\end{align}$$
換言之,只有那些沒有每個 $\mathbf{k}$ 值上,都佔據著電子的部分填滿能帶(partially filled band),才能夠貢獻電流密度。從費米面(Fermi surface)來看,我們可由所謂的電子袋(electron pocket)或電洞袋(hole pocket)得知那些未填滿能帶中的電子,究竟在 $\mathbf{k}$ 空間中佔據著哪些區域。(圖二)為矽於 $\mathbf{k}$ 空間中的等能量面,差不多就是它的費米面。
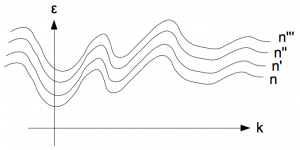
(圖二)所說的等能量「面」也可以是個等能量橢球。嚴格來說,如果等能量面的定義是等能量的波向量 $\mathbf{k}$ 連線集合,那麼理論上有可能出現每個能帶非常緊鄰彼此的情況,如(圖三)所示。
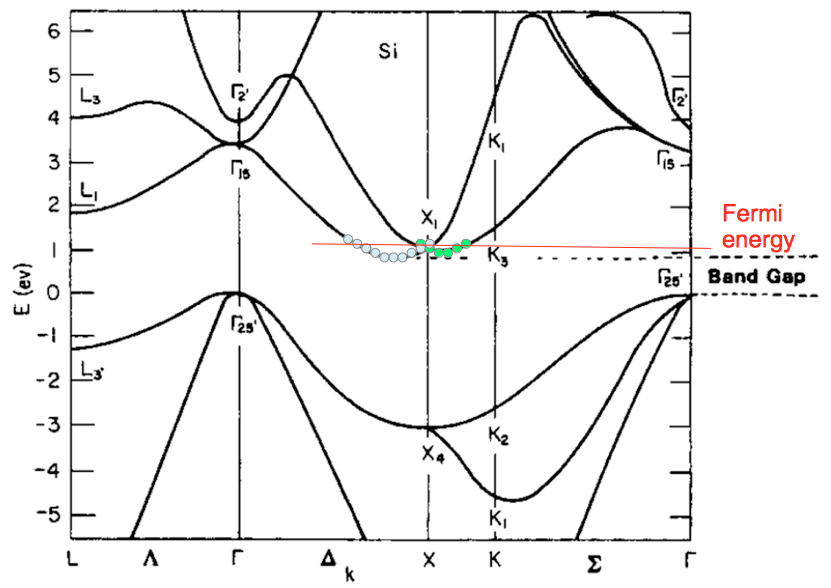
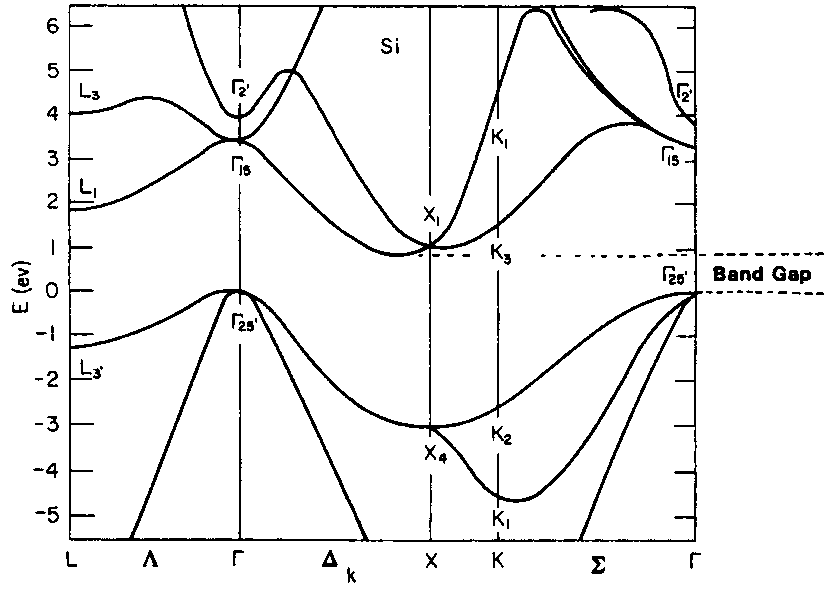
(圖四)矽的真實能帶圖。矽的費米能量(當溫度接近 $0\left.\mathrm{K}\right.$ 時,分隔被填滿能階與未填滿能階的能量)只高於傳導帶最低能量 $\varepsilon_c$ 一點點,所以即便在 X 處有簡併情況發生,但大部分電子應可只考慮擁有最低能量的傳導帶上的電子。也就是說,淺藍色能階數目遠多於綠色能階數目的意思。也可由(圖五)看見原始的、尚未被畫上圓形能階標記的圖案(點圖可至圖片原始連結)
從(圖四)與(圖五)可以發現,雖然理論上每個能帶之間的間隔可以如(圖三)那樣地小,彼此那樣地靠近,但實際上每個能帶之間的距離可說是相當遠。
不過,如果我們討論最廣義的例子的話,確實可以考慮能帶十分緊密的情況(圖三),我們可以將(圖三)想成是(圖四)或(圖五)的鉛直壓縮版本(雖然每個能帶可能還是不會疊得很近,因為每個能帶的極大極小值可能都只落在自己能帶的範圍內,而沒有落在其他能帶的能量範圍內)。
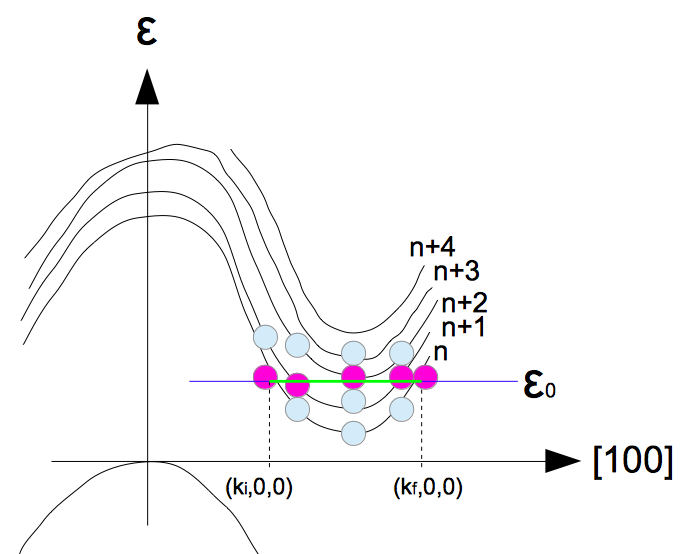
倘若以能帶十分緊密的圖三為例,如果我們畫出能量為 $\varepsilon_0$ 的等能量區域,那麼在 $[100]$ 方向上,你會觀察到有一條由 $(k_i,0,0)$ 指向 $(k_f,0,0)$ 的線段。這就是我們拿一個朝向 $[100]$ 的射線貫穿該橢球中心的痕跡。因此,在這個等能量橢球中,其實涵蓋了位於不同能帶(不同 $n$ 值)的布拉赫電子(Bloch electron)。倘若化學勢比傳導帶的最低能量 $\varepsilon_c$ 還要小(最後我舉的例子是滿足 $\varepsilon_c-\mu\gg k_BT$ 的情況),那麼這些能量高於 $\varepsilon_c$ 的能帶就很難填滿了。因此,佔據圖中所示之 $n$ (含)以上能帶的電子,應該就是對電流密度有所貢獻的電子。
因此,我們要的電子濃度,或者說,單位體積內的電子數目,就是:
$$n\equiv\frac{N}{V}\to n=\sum_{i,\varepsilon_i>\varepsilon_c}\underbrace{f\left(\varepsilon_i=\varepsilon_n(\mathbf{k})\right)\frac{\Delta\mathbf{k}}{4\pi^3}}_{\text{average electron number/ level}}\times\left(\text{number of levels}\right)\tag{10}\label{10}$$
在每個能量下的等能量橢球包住了很多個 $\mathbf{k}$ 空間中的小晶格點($\mathbf{k}=x_1\mathbf{b}_1+x_2\mathbf{b}_2+x_3\mathbf{b}_3$)。而假如每個能帶真的靠得非常接近,那麼每個小晶格點都佔據著一組 $(n,\mathbf{k})$ 數對,亦即每個小晶格點都佔據著兩個能階(基於自旋)。雖然真實的能帶分佈並沒有這麼靠近。接著,如果我們能夠把每個能量大於傳導帶最低能量 $\varepsilon_c$ 的等能量區域所包到的 $(n,\mathbf{k})$ 數對數目,乘上在該能量時,平均每組 $(n,\mathbf{k})$ 數對的電子數目期望值 $f(\varepsilon)\Delta \mathbf{k}/4\pi^3$,那麼就會是在該能帶的小晶格點上的電子數期望值了。
那麼接下來的問題就是,該如何計算在能量為 $\varepsilon_i$ 時,有多少組 $(n,\mathbf{k})$ 數對呢?從(圖二)我們知道,在能量大於 $\varepsilon_c$ 的等能量區域為橢球。因此,只要我們把這些區域的 $(n,\mathbf{k})$ 數目算出來就可以了。在接下來的推導中,我先討論能帶間隔十分小的情況,亦即在等能量橢球中,每個小晶格點 $\mathbf{k}$ 確實都有著一組 $(n,\mathbf{k})$ 數對(對應至兩個能階),接著再來討論矽的真實情況。
而從(圖三)我們可知,在 $n$ 的能帶(就是傳導帶)上,且距離傳導帶最低能量不遠處,它的區域都會維持為橢球形狀(換言之,如果我們考慮能量高於 $\varepsilon_c$ 許多的等能量區域,那它的形狀應該就不會是橢球)。因此,為了方便計算這個區域,我們在數學上平移 $\mathbf{k}$ 空間的原點,平移到使得 $\varepsilon_n(0)=\varepsilon_c$。並在這時,對這個具有最低能量 $\varepsilon_c$ 的能帶能量 $\varepsilon_n(\mathbf{k})$,對最低能量點(即座標原點)作多變數泰勒展開。而在展開之後,為了讓二次項係數變得好看,所以我們再一次地調整 $\mathbf{k}$ 空間的座標軸,把它旋轉到使得下式成立的情況:
$$\frac{\partial^2\varepsilon_n(\mathbf{k})}{\partial k_i\partial k_j}\bigg\vert_{\mathbf{k}=0}=\frac{\partial^2\varepsilon_n(\mathbf{k})}{\partial k_i\partial k_j}\bigg\vert_{\mathbf{k}=0}\delta_{ij}\tag{11}$$
因此,我們的能帶能量對 $\mathbf{k}$ 空間原點做的泰勒展開式即為
$$\varepsilon_n(\mathbf{k})=\frac{\hbar^2}{2}\left(\frac{k_1^2}{m_1}+\frac{k_2^2}{m_1}+\frac{k_3^2}{m_3}\right)+\cdots\tag{12}$$
其中,因為原點是能量最低點的地方,所以它的一次偏微分為零。並且,我們定義三個方向的等效電子質量為 $$\frac{1}{m_i}\equiv\frac{1}{\hbar^2}\frac{\partial^2\varepsilon_n}{\partial k_i^2}\biggr\vert_{\mathbf{k}=0}\tag{13}$$
因為我們是挑具有最低能量 $\varepsilon_c$ 的能帶 $n$ 作泰勒展開,所以可以知道在能量為 $\varepsilon_i>\varepsilon_c$ 時,橢球三軸的半軸長($a$、$b$、$c$)。因此,經過代數代換與體積分後,我們可求得,當 $\varepsilon_i>\varepsilon_c$ 時的 $\mathbf{k}$ 空間等能量區域體積——橢球體積($V_k$)——為:
$$V_k=\frac{4\pi}{3}\frac{m_c^{3/2}\left[2\left(\varepsilon_i-\varepsilon_c\right)\right]^{3/2}}{\hbar^3}\tag{14}$$
其中,等效質量 $m_c$ 定義為 $(m_1m_2m_3)^{1/3}$。而由於我們先討論能帶十分靠近,使得每個小晶格點 $\mathbf{k}$ 上,都以 $\Delta \mathbf{k}=8\pi^3/V$ 的小晶格體積佔據著一組數對 $(n,\mathbf{k})$ 的情況(兩個能階,分別對應兩個自旋)。所以,在能量為 $\varepsilon_i$ 時,數對 $(n,\mathbf{k})$ 的數目為:
$$Q_i\equiv\text{number of (n, k) pairs at }\varepsilon_i=\frac{V_k}{\Delta \mathbf{k}}=\frac{4\pi}{3\Delta \mathbf{k}}\frac{m_c^{3/2}\left[2\left(\varepsilon_i-\varepsilon_c\right)\right]^{3/2}}{\hbar^3}\tag{15}\label{15}$$
接著,將方程式 $(\ref{15})$ 代入方程式 $(\ref{10})$,即可得到:
$$\begin{align}n&=\sum_{i,\varepsilon_i>\varepsilon_c}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}Q_i\tag{16a}\\[4ex]&=\sum_{i,\varepsilon_i>\varepsilon_c}\left[\frac{\Delta \mathbf{k}}{4\pi^3}\frac{1}{e^{(\varepsilon_i-\mu)/k_BT}+1}\right]\left\{\frac{4\pi}{3\Delta \mathbf{k}}\frac{m_c^{3/2}\left[2\left(\varepsilon_i-\varepsilon_c\right)\right]^{3/2}}{\hbar^3}\right\}\tag{16b}\\[4ex]&=\sum_{i,\varepsilon_i>\varepsilon_c}\frac{m_c^{3/2}\left[2(\varepsilon_i-\varepsilon_c)\right]^{3/2}}{3\pi^2\hbar^3}\frac{1}{e^{(\varepsilon_i-\mu)/k_BT}+1}\tag{16c}\end{align}$$
接下來考慮真實的,能帶間隔並沒那麼誇張地小的情況。對於作為本質半導體(Intrinsic semiconductor)的矽,因為它的電子數不夠多,而也因為能帶間隔距離沒那麼小,所以大部分的電子都只集中在具有最低能量的傳導帶的最低點附近(滿足 $\varepsilon_n(\mathbf{k})=\varepsilon_c$ 的第 $n$ 個能帶)。也就是說,化學勢(chemical potential)與傳導帶能量 $\varepsilon_c$ 滿足 $\varepsilon_c-\mu\gg k_BT$ 的情況。因此,我們可以將能量大於 $\varepsilon_c$ 的傳導電子數目期望值,近似為位於傳導帶上的電子數目期望值。以(圖四)所示,就是說淺藍色能階數遠大於綠色能階數的意思。因此,由該傳導帶(能帶量子數為 $n$)的最低點,開始向上計算每個能量 $\varepsilon_i$ 上的 $(n,\mathbf{k})$ 數對數目時:
$$\sum_{i,\varepsilon_i>\varepsilon_c}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}Q_i\approx\sum_{i,\varepsilon_i>\varepsilon_c}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}Q_{i,n}\tag{17}\label{17}$$
其中,$Q_{i,n}$ 為在第 $n$ 個能帶(俗稱的傳導帶)中,能量為 $\varepsilon_i$ 的 $(n,\mathbf{k})$ 數對數目。很巧的是,剛才我們算出的在能量為 $\varepsilon_i$ 的等能量橢球體積所佔據的 $(n,\mathbf{k})$ 數對數目 $Q_{i}$,恰好會是能量從 $\varepsilon_c$ 一直到 $\varepsilon_i$ 的 $Q_{i,n}$ 總和:
$$Q_i=\sum_{j,\;\varepsilon_j>\varepsilon_c}^{i}Q_{j,n}\tag{18}$$
之所以會這樣,是因為其實在各個小晶格點 $\mathbf{k}$ 上,有著許許多多個 $(n,\mathbf{k})$ 數對,也就有其兩倍數目的能階。也就是說,在同樣的 $\mathbf{k}$ 中,隨著不同的 $n$ 值,有不同的能量 $\varepsilon_n(\mathbf{k})$。從其能帶圖也能看得出來,在固定 $\mathbf{k}$ 時,會對應到許多能帶的能量值。因此,我們計算 $Q_{i,n}$ 的方法就是:
$$\begin{align}Q_{i,n}&=\left(\sum_{j}^{i}Q_{j,n}\right)-\left(\sum_{j}^{i-1}Q_{j,n}\right)\tag{19a}\\[4ex]&=Q_{i}-Q_{i-1}\tag{19b}\\[4ex]&=\Delta Q_i\tag{19c}\end{align}$$
因此,我們將它代入方程式 $(\ref{17})$。並且在考慮矽有 $N_e=6$ 個傳導帶橢球的情況下,可以得到
$$\begin{align}n&\approx\sum_{i}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}Q_{i,n}\tag{20a}\\[4ex]&=\sum_{i}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}\Delta Q_{i}\tag{20b}\\[4ex]&=\sum_{i}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}\frac{\Delta Q_{i}}{\Delta \varepsilon_i}\Delta \varepsilon_i\tag{20c}\label{20c}\\[4ex]&\approx\sum_{i}f(\varepsilon_i)\frac{\Delta\mathbf{k}}{4\pi^3}\frac{dQ_{i}}{d\varepsilon_i}\Delta \varepsilon_{i}\tag{20d}\label{20d}\\[4ex]&=\sum_{i}\left(\frac{\Delta \mathbf{k}}{4\pi^3}\frac{1}{e^{(\varepsilon_i-\mu)/k_BT}+1}\right)\frac{d}{d\varepsilon_i}\left[N_e\frac{4\pi}{3\Delta \mathbf{k}}\frac{m_c^{3/2}\left[2\left(\varepsilon_i-\varepsilon_c\right)\right]^{3/2}}{\hbar^3}\right]\Delta \varepsilon_i\tag{20e}\label{20e}\\[4ex]&=\sum_i \frac{N_e m_c^{3/2}\sqrt{2(\varepsilon_i-\varepsilon_c)}}{\pi^2\hbar^3}\frac{1}{e^{(\varepsilon_i-\mu)/k_BT}+1}\Delta \varepsilon_i\tag{20f}\label{20f}\\[4ex]&\approx \int_{\varepsilon_c}^{\infty}\frac{N_e m_c^{3/2}\sqrt{2(\varepsilon-\varepsilon_c)}}{\pi^2\hbar^3}\frac{1}{e^{(\varepsilon-\mu)/k_BT}+1}d\varepsilon\tag{20g}\label{20g}\end{align}$$
其中,方程式 $(\ref{20f})$ 的 $\sum$ 之後的第一項就是常見的狀態密度函數(density of states)$g_c(\varepsilon)$:
$$g_c(\varepsilon)=\frac{N_e m_c^{3/2}}{\pi^2\hbar^3}\sqrt{2(\varepsilon-\varepsilon_c)}\tag{21}$$
$$\to n\approx\int_{\varepsilon_c}^{\infty}g_c(\varepsilon)\frac{1}{e^{(\varepsilon-\mu)/k_BT}+1}d\varepsilon\tag{22}$$
其實我們在方程式 $(20)$ 用了不少近似。第一,在 $(\ref{20c})$ 至 $(\ref{20d})$ 中,因為我們考慮的能階數目變化率 $\Delta Q/\Delta \varepsilon$ 是在極短的能量變化中的變化率,所以可以近似為能階數目對能量 $\varepsilon$ 的瞬間變化率。第二,方程式 $(\ref{20e})$ 是要將所有高於 $\varepsilon_c$ 的 $(n,\mathbf{k})$ 數對上的單位體積電子數加起來,但卻把只有在非常靠近能帶極小值時才成立的橢球體積代入 $Q_i$,之所以這麼做會成立,是因為當 $\mathbf{k}$ 離最低點太遠時,能量就會更高,而這時前面的費米—狄拉克分佈會使得它的貢獻十分靠近零,所以我們就將能量高於 $\varepsilon_c$ 的每個能量下的 $(n,\mathbf{k})$ 數對數目用在傳導帶中,極靠近能帶最低點時的橢球體積中的能階變化數目來近似。而這其實就是最初我們說的,電子都集中在傳導帶最低點附近的意思。最後,在方程式 $(\ref{20f})$ 至 $(\ref{20g})$ 中,由於 $\Delta \varepsilon_i$ 足夠小,所以當我們將 $(\ref{20f})$ 視為黎曼和 $(\ref{20g})$ 時,誤差並不會太大,而這有助於我們接著使用俗稱的波茲曼近似(Boltzmann approximation),將費米—狄拉克分佈近似為:
$$\frac{1}{e^{(\varepsilon-\mu)/k_BT}+1}\approx\;\text{exp}\left[-\frac{\left(\varepsilon-\mu\right)}{k_BT}\right]\tag{23}$$
從而得出我們要的
$$\begin{align}n&\approx\int_{\varepsilon_c}^{\infty}g_c(\varepsilon)\frac{1}{e^{(\varepsilon-\mu)/k_BT}+1}d\varepsilon\tag{24a}\\[4ex]&\approx N_c(T)e^{(\varepsilon_c-\mu)/k_BT}\tag{24b}\end{align}$$
其中,
$$\begin{align}N_c(T)&\equiv\int_{\varepsilon_c}^{\infty}g_c(\varepsilon)e^{-(\varepsilon-\varepsilon_c)/k_BT}d\varepsilon\tag{25a}\\[4ex]&=N_e\frac{1}{4}\left(\frac{2m_ck_BT}{\pi\hbar^2}\right)^{3/2}\tag{25b}\end{align}$$
也許你也有興趣閱讀:
- 〈給一點找指導教授的建議〉
- 〈Sentaurus TCAD 筆記〉
- 〈雪崩光偵測器之崩潰電壓 Python 模擬器〉
- 〈布拉格與勞厄繞射之等價證明〉
- 〈週期位能所帶來的能帶結構——Bloch’s Theorem〉
- 〈什麼是 Density of states?〉

自動引用通知: 半導體元件物理學習書單與心得 | 悟理
自動引用通知: 兩年碩班的 TCAD 學習心得 | 悟理