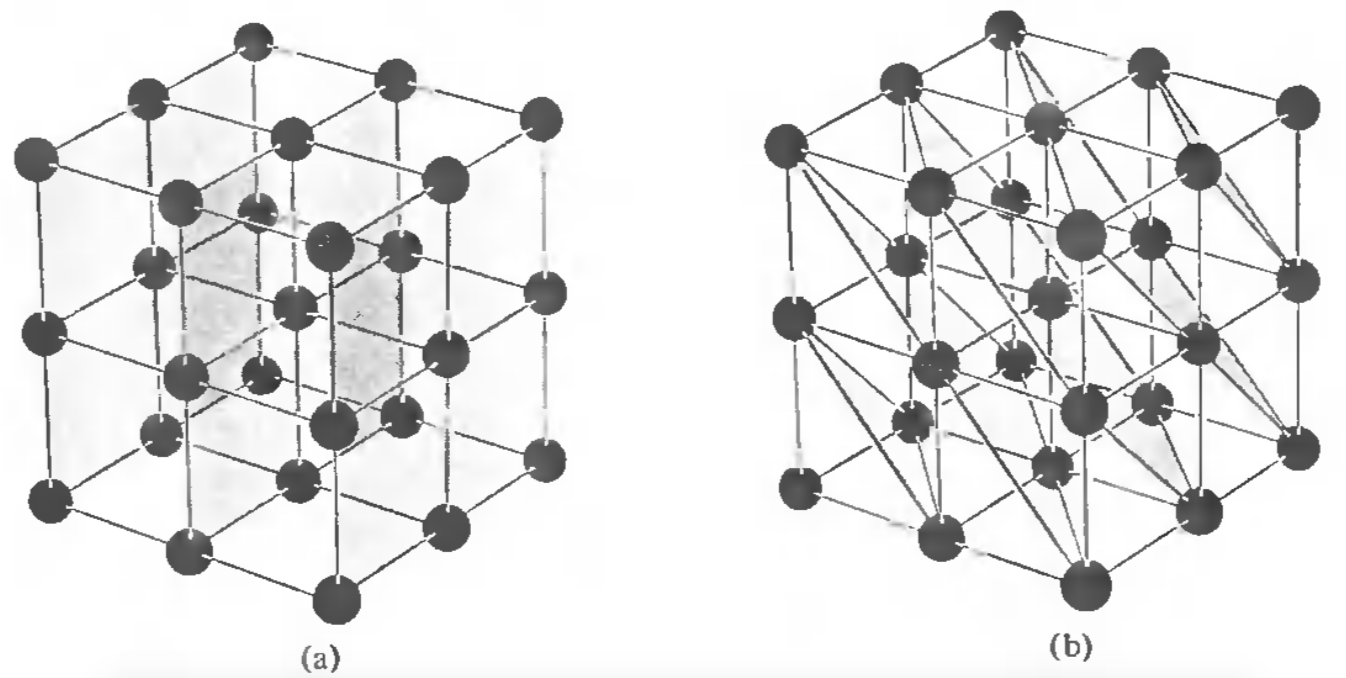
高中時就覺得布拉格繞射的鏡面反射條件非常奇怪,畢竟原子怎麼可能知道它能夠與周圍原子形成什麼樣的等效鏡面,甚至進而產生如此有規律的鏡面反射?讀了固態物理才知道,原來我以前都誤以為每個原子只會有一種等效鏡面,實際上,任何晶格面之間都可以構成布拉格繞射,如下圖一。
而對於每一組晶格面而言,特定的入射波有著固定的散射角 $\theta$,即
$$2d\sin\theta=n\lambda\tag{1}$$
雖然對於有著多種晶格面的察覺使我不再覺得「鏡面反射假設」很奇怪,但我還是覺得有點怪怪的,好像看不太清楚這些波動互相干涉的過程。直到讀了勞厄繞射,我才覺得這一切比較理所當然了點。我希望能在這篇文章分享我對布拉格繞射與勞厄繞射的了解,這兩者真的是非常漂亮的繞射形式。此外,我覺得如果我們從勞厄繞射的角度切入了解晶體結構,那麼會更容易接受所謂的倒晶格(reciprocal lattice)的概念。不過因為我只從 Ashcroft & Mermin (A&M)的固態物理稍微學學繞射,所以一定有所疏漏,還請多多包涵。底下內容完全來自我對 A&M 的消化理解,有興趣的讀者可以參考 A&M 的 〈Ch.5 The Reciprocal Lattice〉 與 〈Ch.6 Determination of Crystal Structures by X-ray Diffraction〉
布拉格繞射
相信進來讀這篇文章的讀者應該已很熟悉高中對布拉格繞射的介紹。除了在前言稍微提及的內容外,我只想特別強調一下布拉格繞射中的論證結構:
- 前提一:某道 X 光被連續的晶格面”鏡面反射”。
- 前提二:某道 X 光的鏡面反射光”皆”經歷了建設性干涉。
- 前提三:波長不隨反射而改變,也就是說,X 光經歷彈性散射。
- 結論:該道 X 光的散射光強度在該鏡面反射方向上,有著局域極大值。
我們可以將此處的前提理解為所謂的「假設」(assumptions),畢竟我們並無法那麼直接地,用肉眼去驗證前提一與二,但倘若我們假設這兩個前提都成立,那麼按照布拉格的推論,我們會在該角度看見布拉格峰值。因此,使我們相信前提一與二成立的好理由,僅僅是其結論的成立——觀察到布拉格峰值。就好比我們從未看見重力、正向力這玩意兒,但基於牛頓定律對常見運動預測的可靠程度,我們似乎有好理由相信牛頓物理理論中的力量的實在性(真實性)。此外,在布拉格繞射的脈絡中,前提一的「鏡面反射」條件是一個沒有被交待由來的假設。某種程度上,前提一是一個獨立於當前物理理論之外的特例假設(ad hoc assumptions)。
勞厄繞射
勞厄繞射是德國科學家馬克斯·馮·勞厄(Max von Laue)於1912年所提出,其與布拉格繞射的差別在於勞厄繞射理論並不需針對繞射現象持有像是「鏡面反射條件」那樣的外圍假設——或說特例假設——從而防止其理論變成一個錯誤的理論。勞厄繞射是奠基於物理學界對晶體結構的基本認知之上的:晶體是由多個週期排列的原子所組成的結構。此外,每個原子可以將任何一個入射波散射到所有方向上。並且,基於常見的波動理論,當這些原子散射的波皆彼此經歷了完全建設性干涉時,我們就能在該方向上觀察到繞射強度的局域極大值。
- 前提一:晶體即為位於布拉菲晶格(Bravais lattice)上的諸多原子所構成的集合。
- 前提二:每個原子都會將任何方向的入射波散射至任何方向上。
- 前提三:朝向某方向上的散射波彼此經歷了完全建設性干涉。
- 前提四:X 光經歷波長沒有顯著變化的彈性散射。
- 結論:在該方向上會出現繞射強度的局域極大值。
先以兩個原子散射為例,考慮從極遠處朝向 $\hat{n}$ 入射的 X 光,如下圖二。
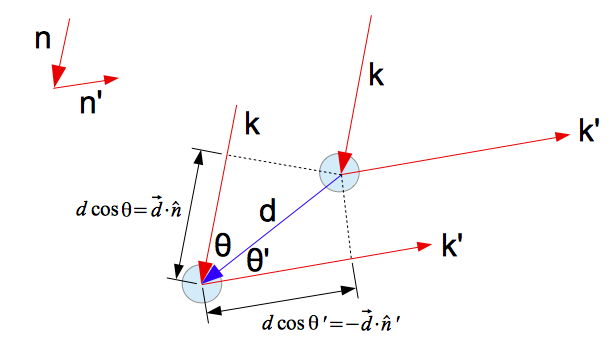
(圖二)入射光由極遠處朝向 $\hat{n}$ 前進,並被原子散射至各個方向中。而在此圖,我們考慮一道被散射至 $\hat{n}’$ 方向的散射光。此外,這兩者原子位於布拉菲晶格中,$\vec{d}$ 表示它們的相對位置向量。入射光與散射光的波向量分別為 $\vec{k}$ 與 $\vec{k}’$。
假設這兩道散射波彼此經歷完全建設性干涉,那麼其波程差必須為波長的整數倍。
$$\frac{d\cos\theta}{\lambda}+\frac{d\cos\theta’}{\lambda’}=m\tag{2}\label{2}$$
由於我們假設波長並沒有顯著變化,所以 $(\ref{2})$ 可以基於 $\lambda’\approx\lambda$ 以及使用內積表示法而簡化為:
$$\vec{d}\cdot(\hat{n}-\hat{n}’)\approx m\lambda\tag{3}\label{3}$$
為了引入波向量 $\vec{k}$,讓我們將 $(\ref{3})$ 兩邊同乘 $2\pi/\lambda$,可以得到:
$$\vec{d}\cdot(\vec{k}-\vec{k}’)\approx 2\pi m\tag{4}$$
在考慮完簡單的兩個散射原子情況後,我們接著要求每個原子的散射波,彼此都經歷了完全建設性干涉。由於我們在前提一假設了每個原子都位於布拉菲晶格點上,所以每個原子之間的相對位置 $\vec{d}$ 都可由 $\vec{R}=n_1 \vec{a}_1 + n_2 \vec{a}_2 + n_3 \vec{a}_3$ 表示。因此,我們進一步要求能夠被觀測到局域繞射極大值的散射波向量 $\vec{k}’$ 滿足下列條件:
$$\vec{R}\cdot(\vec{k}-\vec{k}’)\approx 2\pi m\tag{5}\label{5}$$
此為所謂的「勞厄方程式」(Laue equations)。值得注意的是,這個特定的散射波向量 $\vec{k}’$ 不只滿足一個特定的 $\vec{d}$,而是對於任何的布拉菲晶格向量 $\vec{R}$ 都必須滿足 $(\ref{5})$,這是一個非常嚴格的條件。只有這種散射波 $\vec{k}’$ 會發生在局域繞射極大值上。當然,對於不同的布拉菲向量 $\vec{R}$,可以有著不同的整數 $m$,畢竟不論是哪個整數,都代表著完全建設性干涉的要求。進一步而言,我們可以將 $(\ref{5})$ 等價地改寫為下式:
$$\begin{align}e^{i(\vec{k}’-\vec{k})\cdot\vec{R}}\approx 1,&\quad\text{for all Bravais lattice vectors }\textbf{R}.\tag{6}\label{6}\end{align}$$
上式 $(\ref{6})$ 就是著名的倒晶格定義式。
倒晶格的意義
雖然我讀的 Kittel 與 A&M 都是先提倒晶格定義,再接著提繞射條件中蘊涵的倒晶格定義(Kittel 是提散射振幅 scattering amplitude,而 A&M 則是提上述的勞厄繞射條件),但我總覺得如果我們換個順序理解繞射條件與倒晶格定義,或許比較會覺得倒晶格的意義有其價值——為了方便描述能產生完全建設性干涉的波向量變化量。
因此,我對倒晶格的看法是,對於能夠滿足繞射條件 $(\ref{6})$ 的波向量變化量($\Delta\vec{k}\equiv\vec{k}’-\vec{k}$),我們將這種成立完全建設性干涉的波向量變化量 $\Delta\vec{k}$ 所構成的集合稱之為倒晶格,或說倒空間 $\textbf{K}$:
$$\textbf{K}=\{\textbf{K}\;\vert \;e^{i\textbf{K}\cdot\vec{R}}=1,\quad\text{for all Bravais lattice vectors }\textbf{R}\}\tag{7}\label{7}$$
由這些向量所組成的向量空間則稱為倒空間。而之所以有「倒」這個字,無非是因為 $\textbf{K}\cdot\vec{R}=2\pi m$ 使得 $\textbf{K}$ 在某種意義上是實晶格 $\vec{R}$ 的倒數。藉由倒晶格的定義,我們也可重新詮釋 $(\ref{6})$,我們說那些產生完全建設性干涉的波向量變化量 $\Delta\vec{k}$,恰好為倒晶格中的一個向量。
Constructive interference will occur provided that the change in wave vector, $\textbf{K}\equiv\vec{k}’-\vec{k}$, is a vector of the reciprocal lattice. (A&M p.99)
此外還有另一種勞厄繞射幾何詮釋。首先我們用 $\textbf{K}$ 表示倒空間(k space)中的向量,也就是由倒空間原點指向任意倒晶格點的向量。而對於那些發生完全建設性干涉的散射波,其波向量變化量 $\Delta\vec{k}\equiv\vec{k}’-\vec{k}$ 恰好為倒空間中的倒晶格向量(滿足$(\ref{6})$),所以我們可以定義一個倒晶格向量 $\textbf{K}$ 為 $-\Delta\vec{k}$。之所以有個負號,是為了讓我們待會能得到較符合直覺的幾何圖像。讀者可試試看沒有負號的定義,按照底下脈絡推論,就可了解如此選擇的意義。重要的是,不論 $\textbf{K}$ 的定義有無負號,$\textbf{K}\equiv\pm\Delta\vec{k}$ 都使得波向量變化量 $\Delta\vec{k}$ 滿足 $(\ref{7})$ 的倒空間(或說倒晶格)定義,從而等價地滿足 $(\ref{6})$,這是唯一的要求。因此,我們可將散射波向量 $\vec{k}’$ 改寫為:
$$\vec{k}’=\vec{k}-\textbf{K}.\tag{8}\label{8}$$
又因為我們假設此為彈性散射,波長變化量是可忽略的,所以可得:
$$\vert\vec{k}’\vert=\vert\vec{k}\vert\quad\to\quad \vert \vec{k}\vert=\vert\vec{k}-\textbf{K}\vert\tag{9}\label{9}$$
在我們將 $(\ref{9})$ 兩側取其平方後,可以化簡為:
$$\vert \vec{k}\vert^2=\vert \textbf{K}\vert^2-2\textbf{K}\cdot\vec{k} + \vert\vec{k}\vert^2\quad\to\quad \frac{1}{2}\vert\textbf{K}\vert = \vec{k}\cdot\hat{K}\tag{10} $$
而這結果的幾何意義就是,倘若我們將入射波向量 $\vec{k}$ 的尾端置於倒空間原點上,並且其箭頭恰好落於某倒晶格向量 $\textbf{K}$ 的中垂面上時,那麼我們可由此得知:在這入射波造成的諸多散射波 $\vec{k}’$ 中,唯有其波向量恰好為從倒晶格向量 $\textbf{K}$ 之箭頭指向入射波向量箭頭 $\vec{k}$ 的散射波($\because \textbf{K}=-\Delta\vec{k}$),才能夠產生完全建設性干涉,如下圖三所示。而這種位於倒空間中的中垂面被稱為「布拉格面」。
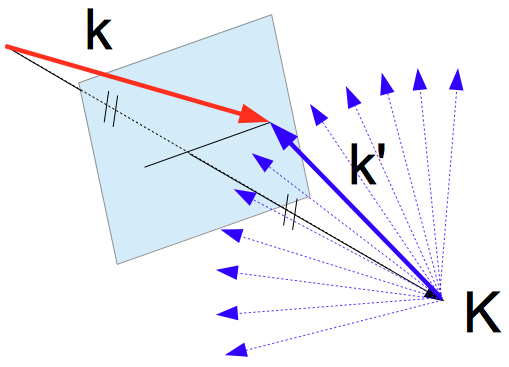
(圖三)黑線為倒晶格空間中的某個晶格向量,淺藍色平面為其中垂面。雖然紅色的入射波向量 $\vec{k}$ 必然會產生各種方向的彈性散射波 $\vec{k}’$,如藍箭頭所示(約略相同的藍箭頭長度表示彈性散射的能量守恆條件),然而,只有粗實線的藍箭頭才能夠產生完全建設性干涉,至於其他方向與的彈性散射波向量則不會構成完全建設性干涉,也就沒辦法在該散射方向上觀察到光強度局域極大值。
事實上,這種勞厄繞射的幾何圖像恰好就是布拉格繞射觀點的體現,只要我們能夠找到這位於倒空間中的布拉格面與實空間中的晶格面的關係,就可理解布拉格繞射與勞厄繞射的等價性。
晶面族與倒晶格向量的關係
即便我早在半年前就詳讀了底下命題於 A&M 固態物理的證明,間斷讀了不下十次,但我到現在還是覺得有點混亂,似懂非懂。其實這也是為什麼我想寫這篇文章的原因,我始終覺得這證明才是一切的精華所在。只要懂了這個證明,那麼真實的晶格面族與倒晶格的關係似乎就呼之欲出了。所以什麼是晶格面族呢?
所謂的晶(格)面族(family of lattice planes),就是一群相互平行、等間距並相切所有三維布拉菲晶格點的平面所構成的集合。任何一個晶格面都必然對應到其中一個晶面族。而顯然地,三維布拉菲晶格可以有著非常多種晶面族,如下圖四。底下的命題可以讓我們藉由倒晶格向量為所有可能的晶面進行相當簡單的分類。
(1) 對於任何間距為 $d$ 的晶面族,一定存在著垂直於這些晶面的倒晶格向量,其中最短的倒晶格向量長度為 $2\pi/d$。反之,(2) 對於任何一個倒晶格向量 $\textbf{K}$,一定存在著一個與其垂直且間距為 $d$ 的晶面族,其中,$2\pi/d$ 為平行於 $\textbf{K}$ 的最短的倒晶格向量。見圖五。
接下來的任務就是依序證明命題 (1) 與 (2)。先從 (1) 開始:
(1) 對於任何間距為 $d$ 的晶面族,一定存在著垂直於這些晶面的倒晶格向量,其中最短的倒晶格向量長度為 $2\pi/d$。
設想一個垂直於 $\hat{n}$、相鄰晶面距離 $d$ 的晶面族,我們接著證明 (1a) $\textbf{K}=2\pi/d\;\hat{n}$ 為倒晶格向量,以及 (1b) 在 $\hat{n}$ 上,不可能有著比它更短的倒晶格向量。針對 (1a),對於通過實晶格原點的晶面,因為 $e^{i\textbf{K}\cdot\vec{0}}=1$,並且此晶面上每個晶格點的位置向量必然垂直於 $\textbf{K}$,所以:
$$e^{i\textbf{K}\cdot\vec{r}_0}=1,\quad\text{for all points }\vec{r}_0\text{ on the lattice plane which passes the origin.}$$
接著,其他晶面上的晶格點的位置向量,可以藉由將它們平移整數個間隔向量 $d\;\hat{n}$ 來表示:
$$\vec{r}_m=\vec{r}_0+m\cdot d\;\hat{n}\tag{11}\label{11}$$
對於這些點,我們可以得出以下結果:
$$\begin{align}e^{i\textbf{K}\cdot\vec{r}_m}&=e^{i\textbf{K}\cdot\vec{r}_0}\times e^{i\textbf{K}\cdot m\hat{d}}\tag{12a}\\[5pt]&=1\times e^{i\cdot 2\pi m}\tag{12b}\\[5pt]&=1\tag{12c}\end{align}$$
因此,向量 $\textbf{K}=2\pi/d\;\hat{n}$ 使得所有三維布拉菲晶格點 $\vec{R}$ 都滿足 $e^{i\textbf{K}\cdot\vec{R}}=1$,即 $\textbf{K}$ 為倒空間中的元素(參見 $(\ref{7})$),所以 $\vec{K}$ 必為倒晶格向量。接著是證明 (1b),讓我們假設有著比 $\textbf{K}=2\pi/d\;\hat{n}$ 還要短的倒晶格向量,例如 $\textbf{K}’\equiv 2\pi/d’\;\hat{n}$,其中 $d<d’$。接著我們代入 $(\ref{7})$,檢驗它是否存在於倒空間的向量集合中。針對前述的晶面族,我們用 $\vec{r}=\vec{r}_0+m\cdot d\;\hat{n}$ 表示其每個晶格點的位置向量,由此可得:
$$ \begin{align} e^{i\textbf{K}’\cdot\vec{r}}&=e^{i\textbf{K}’\cdot (\vec{r}_0+m\cdot d\;\hat{n})} \tag{13a}\\[5pt]&= 1\times e^{i\cdot 2\pi m d/d’}\tag{13b} \end{align}$$
因為 $0<d<d’$,所以必然存在著一些晶面,使得 $md/d’$ 不為整數,例如 $m=1$ 的晶面上的晶格點必然使得 $\textbf{K}’$ 無法屬於倒空間的集合 $(\ref{7})$ 中,由此得證不存在著比 $\textbf{K}=2\pi/d\;\hat{n}$ 還要短且與該晶面垂直的倒晶格向量。再來是證明 (2):
(2) 對於任何一個倒晶格向量 $\textbf{K}$,一定存在著一個與其垂直且間距為 $d$ 的晶面族,其中,$2\pi/d$ 為平行於 $\textbf{K}$ 的最短的倒晶格向量。
首先我們考慮一個任意的沿著 $\hat{n}$ 的倒晶格向量 $\textbf{K}$,對於垂直於此向量的所有實空間位置向量 $\vec{r}_0$,兩者內積必為 $0$,並將所有的 $\vec{r}_0$ 集合稱為第 $0$ 面,所以:
$$e^{i\textbf{K}\cdot\vec{r}_0}=1\tag{14}$$
進一步而言,那些平行於第 $0$ 面的所有實空間平面(不一定是晶格面),都可以視為將第 $0$ 面沿著 $\hat{n}$ 平移 $x$ 單位的結果,所以可將它們的位置向量寫為 $\vec{r}=\vec{r}_0 + x\;\hat{n}$,$x\;\hat{n}$ 用以表示平移向量。由於 $\textbf{K}$ 是倒晶格向量,所以其蘊涵的 $\vec{r}$ 必須是滿足 $(\ref{7})$ 的那些向量:
$$\begin{align} e^{i\textbf{K}\cdot (\vec{r}_0+x\;\hat{n})}&=1\times e^{i\textbf{K}\cdot\hat{n}\;x}\tag{15a}\\[5pt]&= e^{iKx} \tag{15b}\\[5pt]&=1\tag{15c}\label{15c}\end{align}$$
因此,$x=2\pi m/K$,其中 $m$ 為使 $(\ref{15c})$ 成立的整數。既然我們找出了所有滿足 $\textbf{K}$ 與 $(\ref{7})$ 的實空間內的平面,那麼接下來要檢查的就是,這些實空間平面中,是否包含著晶格面?假設我們將座標平移至使得有個晶格點的座標為 $\vec{r}=\vec{0}$,那麼我們可使用與 $(\ref{11})$ 完全相同的表達式,那麼因為 $(\ref{11})$ 中的所有晶格點必然滿足 $(\ref{7})$,所以在 $\vec{r}=\vec{r}_0 + x\;\hat{n}$ 實空間平面集合中,確實包含著所有的布拉菲晶格面。最後我們證明,倘若 $\textbf{K}$ 對應到的是間距為 $d$ 的晶面族,那麼與其平行的最短倒晶格向量長度為 $2\pi/d$,亦即 $K\geq 2\pi/d$。
根據 $(\ref{11})$,我們得知
$$e^{i\textbf{K}\cdot (\vec{r}_0+m\cdot d\;\hat{n})}=1\tag{16}$$
因此,在代入 $\textbf{K}\cdot\vec{r}_0=0$ 的條件後,我們得出
$$e^{im\cdot Kd}=1\tag{17}\label{17}$$
因為 $(\ref{17})$ 是指對於第 m 個平行於第 $0$ 面的晶面而言,$\textbf{K}$ 也必須是倒晶格向量,所以倘若 $Kd$ 比 $2\pi$ 還要小,那麼對於第一個($m=1$)平行於第 $0$ 面的晶面而言,$e^{i\cdot 1\cdot Kd}$ 就不可能是 $1$ 了,所以 $Kd\geq 2\pi$,因此得到 $K\geq 2\pi/d$ 的結論。上述的證明讓我們確定,任何一個方向上的最短倒晶格向量必然對應著實晶格中的一個晶面族,反之亦然。最後還有個命題有待我們證明,就是關於那些不具有最短長度的倒晶格向量的性質。
任何一個倒晶格向量 $\textbf{K}$ 的長度,必然是與其平行的最短倒晶格向量 $\textbf{K}_0$ 的整數倍。
讓我們用反證法來證明這命題。首先假設一個倒晶格向量 $\textbf{K}$,它的長度為與其平行的最短倒晶格向量 $\textbf{K}_0$ 的 $N+x$ 倍,其中 $N$ 為正整數,並且 $0<x<1$。
$$\textbf{K}=(N+x)\textbf{K}_0\tag{18}\label{18}$$
由於倒晶格也是布拉菲晶格,亦即滿足加法封閉性(closure under addtion):
$$e^{i\textbf{K}_1\cdot\textbf{R}}=1,\;e^{i\textbf{K}_2\cdot\textbf{R}}=1\quad\to\quad e^{i(\textbf{K}_1\pm\textbf{K}_2)\cdot\textbf{R}}=1\tag{19}\label{19}$$
因此,我們可由 $(\ref{18})$ 與 $(\ref{19})$ 推得,必然也存在著 $\textbf{K}’=x\textbf{K}_0$ 的倒晶格向量。然而,因為 $\textbf{K}’$ 顯然比 $\textbf{K}_0$ 還要短,所以與假設矛盾(注意:先前我們已經證明過最短的長度必然為 $K_0=2\pi/d$),所以得證,任何倒晶格向量的長度,必然為與其平行之最短倒晶格向量的整數倍。
布拉格繞射與勞厄繞射的等價性
我們在 $(\ref{6})$ 與 $(\ref{7})$ 了解到,根據勞厄繞射,倘若有個入射波在被整個晶體彈性散射($\lambda\approx\lambda’$)後,經歷了完全建設性干涉的波向量變化量 $\Delta\vec{k}$,那麼 $\Delta\vec{k}$ 必然可以是倒空間中的一個倒晶格向量。因此,讓我們定義一種倒晶格向量 $\textbf{K}\equiv\Delta\vec{k}=\vec{k}’-\vec{k}$。值得注意的是,這與我們先前為了引入布拉格面所定義的 $\textbf{K}$ 差了一個負號。如此定義或許不是很方便理解先前提到的「中垂面示意圖」,但卻適合用來理解布拉格繞射與勞厄繞射的等價性,如下圖六。
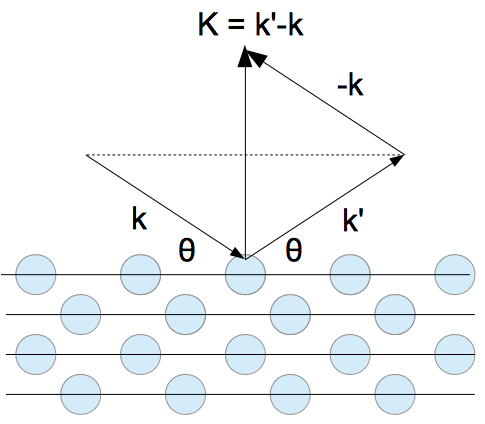
(圖六)繞射面示意圖。根據前述理論,任意晶面族必然在該法線方向上存在著倒晶格向量 $\vec{K}$。在此,入射波向量為 $\vec{k}$,散射且經歷完全建設性干涉的波向量為 $\vec{k}’$,並且繞射角為 $\theta$。
根據剛才證明的定理,勞厄繞射中的 $\textbf{K}\equiv\Delta\vec{k}$ 必然對應著與其垂直的晶面族(注意,這裡的 $\textbf{K}=\Delta\vec{k}$ 只包含經歷完全建設性干涉的散射過程),而這 $\textbf{K}$ 向量的長度必然為與其平行之最短倒晶格向量 $\textbf{K}_0=2\pi/d\;\hat{n}$ 的整數倍。所以我們可以寫下:
$$\vert\textbf{K}\vert=\frac{2\pi n}{d}\tag{20}\label{20}$$
此外,因為此處的 $\textbf{K}\equiv\Delta\vec{k}$,所以:
$$\vert\textbf{K}\vert=\vert\Delta\vec{k}\vert=2\vert\vec{k}\vert\sin\theta\tag{21}\label{21}$$
在將 $(\ref{20})$ 與 $(\ref{21})$ 畫上等號後,可以得到:
$$2\vert\vec{k}\vert\sin\theta=\frac{2\pi n}{d}\tag{22}$$
代入 $\vert\vec{k}\vert = 2\pi/\lambda$,可以得到
$$2\left(\frac{2\pi}{\lambda}\right)\sin\theta=\frac{2\pi n}{d}\quad\to\quad 2d\sin\theta=n\lambda\tag{23}$$
因此,與倒晶格向量 $\textbf{K}$ 對應的勞厄繞射,等價於,與垂直於 $\textbf{K}$ 的晶面族進行鏡面反射的布拉格繞射。而布拉格的繞射階數 $n$ 則為該倒晶格向量 $\textbf{K}=\Delta\vec{k}$ 與其最短平行向量 $\textbf{K}_0$ 的長度比值。


自動引用通知: 兩年碩班的 TCAD 學習心得 | 悟理
自動引用通知: 半導體元件物理學習書單與心得 | 悟理