已知有一繩綁一物，相對圓心 O 作角速率恆為 $\omega$ 的等速率圓周運動，另一端繫於天花板上，如右圖所示。請問，相對於天花板上的繩的固定點 P 的角速率為何呢？（假定繩長為 $L$，錐動擺角度為 $\varphi$）與此相關的問題是，已知繩長、擺角、相對 O 的角速率，然後求相對 P 點的角動量。
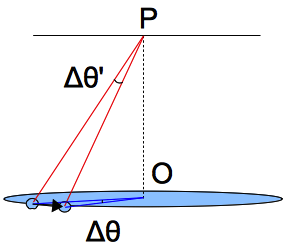
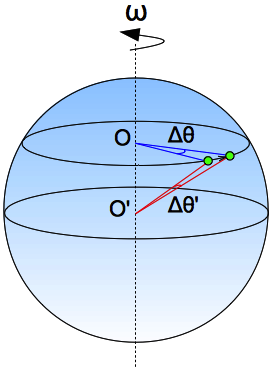
另一種題型是，有一物在緯度 45 度的地方，隨著地球自轉而相對自轉軸作角速率為 $\omega$ 的等速率圓周運動，如左圖。請問該物體對地心的角動量為何？而這可能也涉及角速度的相對性質。雖然我們可藉由 $L=rmv\sin\theta$ 直接迴避角速度的相對問題，但我仍覺得同時掌握 $L=mr^2\omega$ 是值得的，相信這有助於我們了解角動量的概念。
這篇文章將仔細說明角速度的相對性質，希望可以解決同學的疑惑！
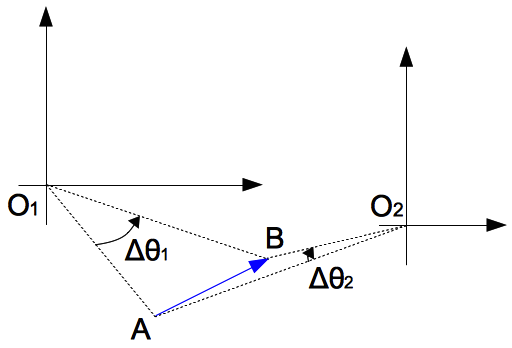
首先來看看一個簡單的 AB 直線運動（如圖一）。O1 與 O2 觀察到的角位移確實不同，但因角位移皆不為零，所以儘管它是沿著直線運動的，但相對 O1、O2 而言仍然是「旋轉運動」。
（圖一）O1 與 O2 為兩觀察者，一物體由 A 點移動至 B 點。此外，兩觀察者與物體起點、終點的連線皆在同一平面上。
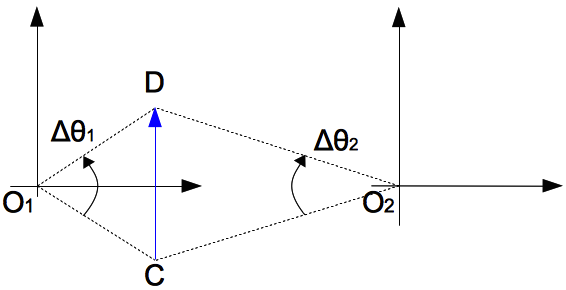
當然了，如果要知道 ∆θ1 與 ∆θ2 的關係，那我們還必須知道對 O1、O2 而言的起點與終點距離。不過，目前我們要處理的問題都有個簡單的性質（見圖二），就是不論是對 O1 還是 O2，物體離他們的距離都是保持固定、不隨時間改變的。
（圖二）物體由 C 點移動至 D 點，其起點與終點分別與兩觀察者的距離恰好是相同的。
由於先前遇到的問題都是作圓周運動，所以都滿足這樣的條件。不過，由於我們討論的不是平均角速度，而是瞬時角速度，所以接著要想像當時間間隔趨近於零時，這兩角位移的量值關係為何[1]。
（圖三）當運動時間歷程(∆t) → 0 時，瞬間位移量值(CD) ≈ R1∆θ1 ≈ R2∆θ2
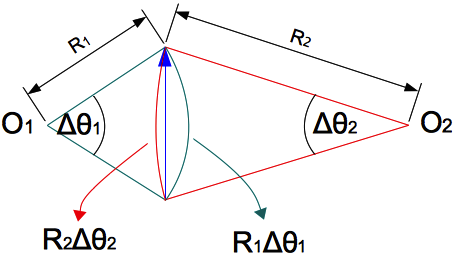
雖然目前看來，我們不能將位移量值近似為（圖三）中的 O1 與 O2 對應的兩弧長，但是在運動時間歷程(∆t) → 0 時，它們確實是幾乎相同的：
$$\overline{CD}\approx R_{1}\Delta\theta_{1}\approx R_{2}\Delta \theta_{2}\tag{1}$$
所以，將上式代入瞬時速率定義式裡頭，我們就能得到：
$$\left|\vec{v}\right|=\lim_{\Delta t\rightarrow 0}\frac{\overline{CD}}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{R_{1}\Delta\theta_{1}}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{R_{2}\Delta\theta_{2}}{\Delta t}\tag{2}$$
最後，在我們處理的圓周運動裡，物體與觀察者的距離是固定的[2]，所以可將 R1 與 R2 提出，最後就得到了該物體分別對觀察者 O1 與 O2 的相對角速度大小關係式：
$$R_1\lim_{\Delta t\to0}\frac{\Delta\theta_1}{\Delta t}=R_2\lim_{\Delta t\to0}\frac{\Delta\theta_2}{\Delta t}\tag{3}$$
$$\therefore R_1\omega_1=R_2\omega_2\tag{4}$$
最後，回到一開始的兩個例子。對於錐動擺的例子，我們可得到：
$$L\times\omega_p=L\sin\varphi\times\omega_O\tag{5}$$
因為已知物體對圓心 O 的轉速為 $\omega$，所以由上式得其對 P 點的轉速為 $\omega\sin\varphi$。因此，物體對 P 點的角動量即為：
$$L_p=mL^2\omega\sin\varphi\tag{6}$$
對於地球自轉的例子，我們可以得到：
$$R_E\times\omega_\text{earth,center}=R_E\sin 45^\circ \times\omega_\text{rotation,axis}\tag{7}$$
因為已知物體對地球自轉軸之轉速為 $\omega$，所以由上式可得其對地心的轉速為 $\omega\sin 45^\circ$。因此，物體對地心的角動量即為：
$$L_\text{earth,center}=mR_E^2\omega\sin 45^\circ\tag{8}$$
[1] 在（圖二）中，由於我們通常設定物體逆時鐘旋轉時，其角位置是遞增的，所以 O1 觀察到的角位移是大於零的，而 O2 則是小於零的。
[2] 如果不固定，那麼就要取瞬時速度垂直位置向量的有效分量計算，這稍微需要另外的說明。
Loading ...
有一個問題, 不知你有興趣回答嗎?
一般的速度相加, 可以想成: 若有一車子速度為V, 在車上有一物相對於車子速度為W, 則對靜止者而言該物的速度是V+W
現在改成角速度, 角速度相加時, 也有類似的物理解釋嗎?
謝謝
你好，認真想了想，我覺得角速度應該沒有像是速度那樣的疊加原理，因為角位移不具有這種原理。以這篇文章的圖三為例，對於被固定在地面而保持靜止的 $O_1$ 與 $O_2$ 觀察者而言，倘若有一物 S 之位移為 $\vec{AB}$，並且對兩觀察者分別有 $\Delta\theta_1$ 與 $\Delta\theta_2$ 的角位移。也就是說，
S 對 $O_1$ 之角位移：$\Delta\theta_{S,O_1}=\Delta\theta_1$
S 對 $O_2$ 之角位移：$\Delta\theta_{S,O_2}=\Delta\theta_2$
因此，假設角位移具有位移所擁有的重疊性質，即 $\Delta\theta_{O_2,O_1} = \Delta\theta_{O_2,S} + \Delta\theta_{S,O_1}$。那就表示：
$$\Delta\theta_{O_2,O_1} = -\Delta\theta_2 + \Delta\theta_1$$
由於兩觀察者相對靜止，所以 $\Delta\theta_{O_2,O_1}$ 恆為零，而這就表示 $\Delta\theta_1$ 恆等於 $\Delta\theta_2$，但是這兩角位移並不必然相同，現在圖三的模樣顯然就有著不相同的角位移，所以得證：角位移不具有位移所擁有的重疊性質。
這位移讓我想到「角速度是不是向量」的問題，這在 Marion 力學課本有滿詳細的說明，可能有些關係。Marion 是說，因為角位移不滿足向量加法的交換律，所以角位移並不是向量（除了 infinitesimal angular displacement）。
剛找到的一篇相關文章（沒仔細看）：Is angular velocity a vector or a scalar? Can you explain?
如果有兩個速度V和W, 我們視為理所當地處理 V+W, 但這個加法究竟是什麼意思? 做為速度, 一個質點在同一時刻只能有一個速度, 所以, V和W只好是不同質點的速度; 既然是不同質點的速度, 把它們加起來, 那是什麼東西在相加?
特別是我們理所當然地把一個速度V分解為i方向和j方向, 然後加起來: V=ai+bj; 然而, 這時候的ai和bj分別又是誰的速度呢?
所以, 我認為一般講向量加法的時候, 根本沒有"進入實際情境"!
一個合理的想法應該是這樣, 我們雖然一開始只有一個速度V, 但我們假想它是這樣形成的: 假設這個質點坐在一個以ai速度移動的車子上, 然後在車上、相對於車子做了bj的運動, 這時, 它相對於地面的速度, 就是ai+bj了。
現在把情況換成轉動: 角速度V和角速度W的相加, 應該也是想成賌點相對於轉動中的i, j,k座標, 有一個角速度V, 而i,j,k (做為一個rigid frame) 又同時對靜止空間有一個角速度W; 這時, 從靜止空間看來, 該質點就有一個角速度 V+W了
例如, 我們在地球上定一個i,j,k; 但這組rigid frame有一個角速度, 因為地球繞日的原故 (假設太陽系是靜止的)。這時, 如果有一質點在在地球上相對於i,j,k 有一個角速度 (例如地球自轉), 那麼, 從太陽系看起來, 該質點的角速度應該就是二者的和了—–如果以地球為轉動中心的話。
這件事情, 甚至不須要轉動的中心相合 (地球並不在太陽中心)。
以上的論斷, 我做過初步的推導, 只是不知道對不對?
哈囉，我剛才回覆您了。因為我並非回覆在您這篇留言下方，而是回覆在這篇文章底下，所以並不確定系統有沒有發信通知您我的回覆，特此留言通知您一聲。另外我雖然目前只回覆您第一段，但推薦您先看看我目前的回覆，因為我擔心回覆太多而失焦。
剛才我接著補齊對您後半段留言的想法囉，再請您參考。
感謝你花了很多力氣來回應, 你說的我都同意, 只是到了最後, 關於角位移和角速度的事情, 我的想法是這樣:
1. 一般書上強調角位移不是向量因為沒有交換律, 我以為這並沒有說到事情的要點; 要點並不在交換律 (不然, 好像是數學硬要把交換律內鍵到向量定義裡才造成物理量不能相加), 而在: 當用一向量代表一角位移的時候, 連續做兩個角位移後仍然是一個角位移, 所以它也當然由一向量代表, 可是, 這一代表兩個角位移合成的向量, 卻並不是原本兩代表向量之和。
2. (瞬時)角速度當然是角位移的微分 (這不難計算)
3. 將一個剛體, 或座標frame i,j,k 做一個角位移, 得到i',j',k'時, 兩個frame 之間會有一個轉動矩陣 A(保角保長且行列式為+1) 相聯: [i',j',k']=[i,j,k]A; 這時, 有一個向量w代表A, 若A是時間的函數, 則A的微分在t=0將會是w在t=0的值, A'(0)=w(0), 就是該轉動在t=0的角速度; (AX)'=w x X = v, 萁中X為任一點的位置向量, v為該點的速度, 在t=0
4. 若一個frame 先經過A矩陣轉動, 再經過B矩陣轉動, 則結果會是AB矩陣; 對AB矩陣微分並在t=0取值
就會得到w1+w2, 其中w2當然是B轉動在t=0時的角速度。
理由: (ABX)'=(AX)'B+A(BX)' = w1 x X + w2 x X = (w1+w2) x X, 因為A和B在t=0時都是單位矩陣
非常感謝您的回覆，讓我再花點時間仔細想想這問題，想清楚後再好好回覆與您討論 🙂
您也可在這裡使用 LaTeX 打矩陣哦：
$$\begin{pmatrix}5 \\\\ 1 \\\\ 2\end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\\\ 0 & 1 & 0 \\\\ 0 & 0 & 1\end{pmatrix}\begin{pmatrix}5 \\\\ 1 \\\\ 2\end{pmatrix}\tag{1}$$
不過要注意，本來用以斷行的雙斜線，要改成四斜線，另外也需要雙錢字號。代碼範例如下：
$$\begin{pmatrix}5 \\\\ 1 \\\\ 2\end{pmatrix}\tag{1}$$
剛才的慝名訪客還是我
哈囉您好，不好意思前兩天我剛好外出，不方便用電腦，所以現在才好回覆您：
「如果有兩個速度V和W, 我們視為理所當地處理 V+W, 但這個加法究竟是什麼意思? 做為速度, 一個質點在同一時刻只能有一個速度, 所以, V和W只好是不同質點的速度; 既然是不同質點的速度, 把它們加起來, 那是什麼東西在相加?」
您提到「一個質點在同一時刻只能有一個速度」，這句的意思"好像"是指「物體的運動並不受觀察者所影響」，是嗎？讓我先假設是這意思，那麼我是認同的。在牛頓力學框架下，物體的運動是指動量 $\vec{p}=m\vec{v}$，而動量又僅會受外力所影響。換言之，物體具有慣性。
緊接著您提到「一個質點在同一時刻只能有一個速度」，我也認同您這個想法。不論觀察者為何，對同一觀察者來說，同一物體不能夠既以 $3\left.\mathrm{m}/\mathrm{s}\right.$ 速度向左，又以 $5\left.\mathrm{m}/\mathrm{s}\right.$ 向右，因為物體的位置對時間之函數 $x(t)$ 是唯一的，所以其位置時變率也只能是獨一無二的，即 $v(t)\equiv dx/dt$。
您後來接著提到「所以, V和W只好是不同質點的速度」，這部分我認同，不過我向進一步分享些想法，由此可更了解$V+W$物理意義的由來，也就有助於我說明之所以認為角速度不具有相同運算規則的原因。首先，並不是所有數學計算都具有物理意義，例如說我們知道 A 物重為 $W_A$，而 B 物重為 $W_B$，那麼兩物總重呢？實際上，我們得真的將兩物疊在一起，再一起放置到磅秤上，我們才知道兩物重量。經許多實驗可知，兩物總重 $W_\text{total}$ 剛好是 $W_A+W_B$。就這意義上，我們才能說 $W_\text{total}=W_A+W_B$。然而，有些時候就不能這麼說了，以轉動角位移為例，雖然我們很希望可以用向量來描述角位移，但卻不行。由於需要畫圖解說才較好理解，所以我推薦您讀下列兩篇文章：
高中物理教材內容討論:角位移是向量嗎? – 國立臺灣師範大學物理學系
角位移_百度百科
話說回來，這表示當我們說「有兩個速度V和W, 我們視為理所當地處理 V+W」時，其實它的意義取決於計算者，看我們想怎麼詮釋那條數學。
考慮兩觀察者，分別名為1號與2號，同時觀察著相同的物體——天上那朵雲。如上圖所示，我定義了底下三個物理量：
$X_1$：1號觀察者用以描述任何物體位置的座標軸，並以自身為坐標原點。
$X_2$：2號觀察者用以描述任何物體位置的座標軸，並以自身為坐標原點。
$X_{21}$：1號觀察者用以描述2號觀察者位置的物理量，也就是2號觀察者相對1號觀察者的位置。在上圖中，此物理量為 $X_{21}=+6$，其中的加號是用以"強調"2號觀察者位於1號觀察者之座標值遞增的方向。
$X_\text{cloud,1}$：雲朵相對1號觀察者的位置，即 $X_\text{cloud,1}=+14$。
$X_\text{cloud,2}$：雲朵相對2號觀察者的位置，即 $X_\text{cloud,2}=+8$。
在現階段來說，我們不曉得底下數學運算有無任何物理意義：
1. $\sqrt{X_\text{cloud,1}}-\sqrt{X_\text{cloud,2}}$
2. $X_\text{cloud,1}\times X_\text{cloud,2}$
3. $X_\text{cloud,1}+X_\text{cloud,2}$
4. $X_\text{cloud,1}-X_\text{cloud,2}$
5. $X_\text{cloud,2}-X_\text{cloud,1}$
6. $X_\text{cloud,2}\sqrt{X_\text{cloud,1}}$
但是，如果我們繼續列舉許許多多物理情境，並觀察隨之改變的上述各物理量（$X_{21}$、$X_\text{clound,1}$、$X_\text{clound,2}$）之間的關係，那麼你會發現這三個物理量居然總是滿足底下的關係式：
$$X_\text{object,1}=X_\text{object,2}+X_{21}\tag{1}$$
因此，我們說上式為一條恆等式（identity），那麼該怎麼看待或是「詮釋」這條數學式呢？由於這個關係式告訴了我們「物體對不同觀察者而言的相對位置之間的關係」，所以我們會說，這是一條關於「相對位置」的恆等式。以上述的雲朵為例，這告訴了我們，倘若你知道雲朵相對於2號觀察者的位置，也知道2號相對1號的位置，那麼就可以推得，雲朵相對於1號觀察者的位置。在這意義上，我們說方程式(1)具有物理意義，如此的加法確實有意義。進一步而言，先前提到的 $\sqrt{X_\text{cloud,1}}-\sqrt{X_\text{cloud,1}}$、$X_\text{cloud,1}\times X_\text{cloud,2}$、⋯⋯等運算，雖然有辦法算出數字，但是卻"尚未找到""相對應"的物理意義（其實第四點與第五點具有相對應的物理意義）。
接著搭配變化量 $\Delta$ 的定義，$\Delta\equiv(\cdots)_\text{final}-(\cdots)_\text{initial}$，並繼續觀察研究與推導，就可以得到：
$$\Delta X_\text{object,1}=\Delta X_\text{object,2}+\Delta X_{21}\tag{2}$$
這告訴我們，原來不同觀察者所觀察到的同一物體之位移（$\Delta X$）擁有上述關係，所以上述的運算具有物理意義，所以我們說「可以這麼算！」。接著，我們還是一樣繼續觀察研究與推導，就可以得到：
$$\frac{\Delta X_\text{object,1}}{\Delta t}=\frac{\Delta X_\text{object,2}}{\Delta t}+\frac{\Delta X_{21}}{\Delta t}\tag{3}$$
搭配我們定義的平均速度，$\bar{V}\equiv\Delta X/\Delta t$，可以進一步將方程式(3)改寫為：
$$\bar{V}_\text{object,1}=\bar{V}_\text{object,2}+\bar{V}_\text{21}\tag{4}$$
也就是說，我們可以將速度進行如此這般的加法運算！方程式(4)的物理意義非常顯而易見，就是不同觀察者對同一事件所觀察到的相對速度關係式。
由此我們就可以說，倘若將您最先提及的 $V$ 與 $W$ 詮釋為：
$V$：物體相對2號觀察者的速度
$W$：2號觀察者相對1號觀察者的速度
那麼就可以得到 $V+W$ 的物理意義：物體相對1號觀察者的速度。因此，說回您的第一段：
1. $V$與$W$不見得只能是不同質點的速度，而可以代表著物體相對”2號觀察者的速度”($V$)以及”2號觀察者相對1號觀察者的速度”($W$)。
2. 在上述的$V$與$W$意義下，$V+W$的物理意義就是”物體相對1號觀察者的速度”。
因此，這與您底下所舉的 $a\hat{i}+b\hat{j}$ 例子是一致的。
也就是說，我們可以分別定義 $V_\text{object,car}$ 與 $V_\text{car,ground}$ 為：
$V_\text{object,car}$：物體（object）相對車子的速度，即 $b\hat{j}$。
$V_\text{car,ground}$：車子相對地面（ground）的速度，即 $a\hat{i}$。
因此根據上述推理，可以得到：
$$\begin{align*}V_\text{object,ground}&=V_\text{object,car}+V_\text{car,ground}\\[5pt]&=b\hat{j}+a\hat{i}\end{align*}$$
接著您認為角速度也有著相同的關係：
但是，角速度的關係勢必得來自角位移的關係：
$$\Delta \theta_\text{obejct,1}=\Delta\theta_\text{object,2}+\Delta\theta_{21}\tag{5}$$然而，方程式(5)並不成立，所以沒辦法推得底下的方程式(6)：$$\omega_\text{object,1}=\omega_\text{object,2}+\omega_{21}\tag{6}$$
你費心回應很多，我也寫了很多想法，可惜按了送出後全部消失，明天再重寫
天阿，真是辛苦您了！我以前也這樣過，所以後來我都是先把內容備份在記事本，再按下送出….不好意思，WordPress 網誌仍不是那麼方便。
\overhead{v}
剛才是測試latex,好像不行
$\overhead{v}$ 是這樣嗎
$\vec{v}$、$\bar{v}$、$\hat{v}$，要用兩個錢字符號夾起來哦。代碼分別是 vec{}、bar{}、hat{}
就是 $\vec{v}$、$\hat{v}$、$\bar{v}$。抱歉我還沒研究如何更舒服地輸入 LaTeX….
上圖是輸入 LaTeX 的範例
另外我夾帶圖案的方法是，先把圖案上傳 https://imgur.com，再用 html 語法夾帶它…還滿麻煩的。範例如下：
<img src="https://i.imgur.com/TGNzkl9.png" alt="LaTeX 範例" />
倘若您之後想貼圖，只需要將圖片連結貼上來，我會在後台幫您編輯更改 html 代碼（直接輸入會有問題，因為這個輸入欄內建了一些語法，不能直接顯示 html）。此外如果您想打 LaTeX，也可以先試試用單一錢字符號，前後夾著 LaTeX。倘若失敗，我會再幫您把它修改好。
另外，單錢字符號與雙錢字符號有著不同的效果，單錢字符號是行內模式（in-line mode），雙錢字符號是顯示模式（display style），例如 $\iiint_V\vec{E}\cdot d\vec{S}=\frac{Q}{\epsilon_0}$，以及
$$\iiint_V\vec{E}\cdot d\vec{S}=\frac{Q}{\epsilon_0}\tag{5}$$
以下不是好的解說, 但我想先把主要的結論說一下; 不清楚的地方, 以後再慢慢補:
1. 交待答號及基本假設
令E= [i,j,k] 這個列矩陣代表三維空間的一組基底, 空間中任一點P=xi +yj +zk = EX, 其中X=[x,y,z]^t 為P點的座標行矩陣
設E=E(t) 隨時間改變, 但維持 i(t), j(t), k(t) 仍為orthonormal, 且保持同樣的orientation;
這表示: E(t) = E(0) A(t), 其中A為orthogonal 矩陣, 且行列式為+1;
換言之, E(0) 隨著時間t 做保角保長保手性的轉換, 也就是轉動, 而A(t)為轉動矩陣
設P(0)=E(0)X 為空間中任一點, 它隨著E(t) 轉動到P(t)=E(t)X;
也就是: X這個由x,y,z三個數組成的行向量 (行矩陣) 不變;
也就是P(t) 在任一t時刻, 對於該時刻的frame E(t) 的座標不變
2. 定義角位移
因為 P(t) = E(t)X= E(0)A(t)X, 我們知道經過t時間後, P點用E(0) frame來看的座標為 A(t)X
也可以說: P(0) 被轉動矩陣A(t)送到 A(t)X——如果在E(0)frame中單純用座標來看的話
容易証明: 對於任何行列式為+1的orthogonal 矩陣A, 一定存在有單位向量 u以及角θ,
使AX=(θu) x X, 其中 x 為外積, X為任意行向量
(A一定有一個特徵值為1, u即為相應的特徵向量)
這樣, 我們使可以說經過t時間後, P(0) 被以u為轉軸, 轉了θ角,
而θu可以稱為這一轉動的角位移 (因為θ和u都是由A(t)決定的, 所以它們都是t的函數)
注意: θ(t) u(t) 只代表t=0到t=t之間E和P的角移位, 並不代表E(t)和P(t)實際的變動痕跡
3. 用角位移定義角速度
考慮P(t)在t=0的 (線性) 速度: v = P’(0) = dP/dt (0) = d [E(0) A(t)X]/dt (0) =E(0) A’(0) X
= E(0) (θ(t) u(t) x X)’ (0) = E(0) [θ’(0) u(0)+ θ(0) u’(0)] x X
= E(0) θ’(0) u(0) x X
因為A(0)=I (單位矩陣) , 則有 θ(0)=0, 這使得 u’(0)為何不重要
因為: 速度=(角速度) 外積 (位置向量)是常識; 我們從上面推得的
V= E(0) θ’(0) u(0) x X可知, θ’(0) u(0) 就是一般所謂的角速度
因為上式是對任何P或任何X都成立的, 所以, 這個角速度不是P點的角速度而已,
它其實是, 更是 E=[I,j,k] 這個frame的瞬時角速度, 而且, 更重要的是:
角速度就是角位移的微分
注意: 針對單一點的運動, 談它相對原點的角速度, 是有問題的 (可以任意指定一個轉軸);
必須是針對一個frame (其實也就是一個鋼體) 講角速度才是 well-defined
4. 接下來要講的大概是 (細節容後再補):
如果上述的E(0)本身也在相對於另一個固定的frame 轉動, 而其中涉及另一組轉動矩陣B(t)
也就是一個轉動發生在另一個轉動的系統上; 從靜止frame看來, 兩個轉動的合成會涉及 BA
而(BAX)' = B'AX + BA'X = (角速度1) x X + (角速度2) x X
因為 A(0)=B(0)=I, 而B’(0)X= (角速度1) x X; A’(0)X = (角速度2) x X
換言之, 角速度是可以相加的, 在以上的意義下
(另外, 角位移不能相加的理由, 並不是一般書上說的不交換;
這種說法感覺起來, 好像是因為數學堅持要把交換律內建到向量加法的定義中,
才迫使角位移不符合向量的資格——真正的理由容後補)
非常感謝您的留言與討論，我看到囉，會再仔細想想，找個時間好好回覆您。
您好，我看不懂滿多地方的，此外我以為我最初的回應已經有說明為何下式不成立。不曉得您對於下方回應有什麼看法嗎？是覺得哪裡不正確嗎？
$$\Delta\theta_\text{object,2}=\Delta\theta_\text{object,1}+\Delta\theta_{21}$$
理由如下：
以這篇文章的圖三為例，對於被固定在地面而保持靜止的 $O_1$ 與 $O_2$ 觀察者而言，倘若有一物 S 之位移為 $\vec{AB}$，並且對兩觀察者分別有 $\Delta\theta_1$ 與 $\Delta\theta_2$ 的角位移。也就是說，
S 對 $O_1$ 之角位移：$\Delta\theta_{S,O_1}=\Delta\theta_1$
S 對 $O_2$ 之角位移：$\Delta\theta_{S,O_2}=\Delta\theta_2$
因此，假設角位移具有位移所擁有的重疊性質，即 $\Delta\theta_{O_2,O_1} = \Delta\theta_{O_2,S} + \Delta\theta_{S,O_1}$。那就表示：
$$\Delta\theta_{O_2,O_1} = -\Delta\theta_2 + \Delta\theta_1$$
由於兩觀察者相對靜止，所以 $\Delta\theta_{O_2,O_1}$ 恆為零，而這就表示 $\Delta\theta_1$ 恆等於 $\Delta\theta_2$，但是這兩角位移並不必然相同，現在圖三的模樣顯然就有著不相同的角位移，所以得證：角位移不具有位移所擁有的重疊性質。
首先我定義：$$X\equiv\begin{pmatrix}x\\y\\z\end{pmatrix}\tag{1}$$
$$E(0)\equiv\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}\tag{2}$$因此，
$$P(0)\equiv E(0)X=\begin{pmatrix}x\\y\\z\end{pmatrix}\tag{3}$$
此外，考慮一個轉動矩陣 $A(t)$，使得座標系——相對$X$而言——逆時鐘轉了$\theta$，即
$$A(t)\equiv\begin{pmatrix}\cos\theta&\sin\theta&0\\-\sin\theta&\cos\theta&0\\0&0&1\end{pmatrix}\tag{4}$$
因此，
$$E(t)\equiv E(0)A(t)=\begin{pmatrix}\cos\theta&\sin\theta&0\\-\sin\theta&\cos\theta&0\\0&0&1\end{pmatrix}\tag{5}$$
以上是我理解的各符號意義。接下來是我看不懂的地方：
一、「也就是P(t) 在任一t時刻, 對於該時刻的frame E(t) 的座標不變」
我想我可以理解你說的「X這個由x,y,z三個數組成的行向量 (行矩陣) 不變」，你的意思應該是，$X$向量相對紙面而言是固定的，而相對紙面在旋轉的東西，其實是座標系。而 $P(t)$ 只不過是 $X$ 向量投影在新的 $x$、$y$ 軸上的分量。以我上述舉的 $A(t)$ 為例，此分量為：
$$P(t)\equiv E(t)X=\begin{pmatrix}x\cos\theta+y\sin\theta\\-x\sin\theta+y\cos\theta\\z\end{pmatrix}\tag{6}$$
因此，對於該時刻的座標系，也就是該時刻的 $E(t)$ 而言，$X$ 向量於個座標軸上的分量應該是改變了，不是嗎？為什麼說不變呢？
二、
「容易証明: 對於任何行列式為+1的orthogonal 矩陣A, 一定存在有單位向量 u以及角θ, 使AX=(θu) x X, 其中 x 為外積, X為任意行向量 (A一定有一個特徵值為1, u即為相應的特徵向量)」
你底下留言有提到「AX=(θu) x X，改過來就可以」，那麼所以你想改成什麼呢？抱歉我不確定你的意思。而因為你提到 $u$ 是相對應的特徵向量，所以你的意思是 $Au=1u$ 嗎？也就是說，你是想改成 $(Au)X=(1u)\cdot X$ 嗎？抱歉我真不清楚你的意思。
三、
「考慮P(t)在t=0的 (線性) 速度: v = P’(0) = dP/dt (0) = d [E(0) A(t)X]/dt (0) =E(0) A’(0) X
= E(0) (θ(t) u(t) x X)’ (0) = E(0) [θ’(0) u(0)+ θ(0) u’(0)] x X
= E(0) θ’(0) u(0) x X
因為A(0)=I (單位矩陣) , 則有 θ(0)=0, 這使得 u’(0)為何不重要」
因為你提到「AX=(θu) x X 當然是錯的」，所以上述推導中的
$$E(0) A^\prime (0) X=E(0) [θ(t) u(t) \times X]^\prime (0)$$
似乎就有用到 AX=(θu) x X 的關係式，如下所示，
$$\begin{align*}E(0) A^\prime (0) X&=E(0)[A(t)X]^\prime|_{t=0}\\[5pt]&=E(0)[θ(t) u(t) \times X]^\prime|_{t=0}\end{align*}$$
所以，想請問上述引號「…」內的推導是否就有誤呢？若確實有誤，那麼想請問你想改成什麼樣呢？
發現錯誤: 前文中"2. 用角位移定義角速度'這一段裡面, AX=(θu) x X 當然是錯的—-應該是另一個更複雜的式子, 我在心裡自己張冠李代了, 改過來就可以
我正在詳細寫下來，盡快回覆，你問的都對，有的是前述的錯誤要一起改，關於X那個是我沒講清楚