雖然有一堆主題可以寫,但最近實在太過忙碌,所以只好先挑簡單的來寫XD 很多同學一直都不清楚「弧度 $(\mathrm{rad})$」與「度數 $(^{\circ})$」的差別,因而容易有「$\pi = 180$」的想法,我覺得這樣是不太嚴謹的,所以我想稍微說明以下幾個問題:
- 為什麼一圈是 $360$ 度,或者 $360^{\circ}$?
- 為什麼一圈又是 $2\pi$ 弧度,或者 $2\pi\left.(\mathrm{rad})\right.$?
- 度數與弧度的關係是什麼呢?
為什麼一圈是 $360$ 度,或者 $360^{\circ}$?
如維基百科所言:「之所以採用 $360$ 這數值,是因為它容易被整除。$360$ 除了 $1$ 和自己,還有 $22$ 個真因數($2$、$3$、$4$、$5$、$6$、$8$、$10$、$12$、$15$、$18$、$20$、$24$、$30$、$36$、$45$、$60$、$72$、$90$、$120$、$180$),所以很多特殊的角的角度都是整數」,因此,平常使用的度數都只能呈現角度與角度之間的大小,例如你知道 $90$ 度的角會大於 $30$ 度,而沒辦法將角度與其他物理量連結在一起;就好像在有絕對溫標以前,你只能知道水銀溫度計較高僅表示其溫度較高,而無法得出此溫度與微觀動能的關係。
因此,為了將「角度」與「其他物理量」——其實就是半徑與弧長——連結起來,我們使用了弧度這個單位。
為什麼一圈是 $2\pi$ 弧度,或者 $2\pi\left.(\mathrm{rad})\right.$?
這世界有個我覺得非常奇妙的性質,就是不論圓形的面積為何,其圓周長與直徑的比例永遠是 $3.1415926$ …..,而我們將這比例定義為 $\pi$!不知道我有沒有成功讓你感受到這個奇妙性質的驚奇所在?
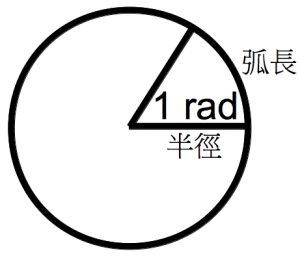
因此,我們就利用這種特別的「圓周長與直徑」關係,或者說「圓周長與半徑」的關係,我們定義所謂的「一弧度」,亦即「$1\left.(\mathrm{rad})\right.$」為:
當弧長等於半徑,此時的角度為 $1\left.(\mathrm{rad})\right.$。
因此,我們就能夠將角度與「世界」連上關係,而不再像是以前的度數,它與我們的「世界」毫無關聯;弧度能連結半徑與弧長,但度數不能。例如:
- 一輪胎往前滾 $50\left.(\mathrm{cm})\right.$,其半徑為 $80\left.(\mathrm{cm})\right.$,請問其轉動角度為何?這答案就是弧長除以半徑,或說弧長與半徑的「比值」,也就是 $$50\left.(\mathrm{cm})\right./80\left.(\mathrm{cm})\right.=0.125\left.(\color{red}{\mathrm{cm}/\mathrm{cm}})\right.=0.125\left.(\color{red}{\mathrm{rad}})\right.$$
- 已知一物繞原點作運動,其角位移為 $2.5\left.(\mathrm{rad})\right.$,並且離原點距離始終為 $10\left.(\mathrm{cm})\right.$。請問此物體之路徑長為何?由於它與原點距離為定值,所以它正在作圓周運動。因此,其路徑長具有「弧長」的意義。由角位移 $2.5\left.(\mathrm{rad})\right.$ 與圓周半徑 $10\left.(\mathrm{cm})\right.$ 可推得弧長為 $$2.5\left.(\color{red}{\mathrm{rad}})\right.\times 10\left.(\color{red}{\mathrm{cm}})\right.=2.5 \left.(\color{red}{\mathrm{cm}/\mathrm{cm}})\right.\times 10\left.(\color{red}{\mathrm{cm}})\right.=25\left.(\color{red}{\mathrm{cm}})\right.$$
由於弧度的定義是弧長與半徑的比值,所以弧度的單位,$\mathrm{rad}$,也就是兩長度單位的比值。有的時候我們又會說它沒有單位,而這只是因為兩個長度單位可以消掉變得沒有單位。根據國際單位制導出單位,弧度的國際單位制表示法為:
$\left.\mathrm{rad}\right.=\left.\mathrm{m}/\mathrm{m}\right.$
舉例而言,若物體每秒角位移為 $\omega=3\left.(\mathrm{rad}/\mathrm{s})\right.$,那麼根據國際單位制,我們又能改寫為 $\omega=3\left.(\mathrm{m}/\mathrm{m})/\mathrm{s}\right.$。若將兩個長度單位消去,就會得到 $\omega=3\left.(\mathrm{rad}/\mathrm{s})\right.=3\left.(\color{rad}{1/\mathrm{s}})\right.=3\left.(\color{red}{\mathrm{Hz}})\right.$。因此,角速度又叫做角頻率。
度數跟弧度的關係是什麼呢?
它們的共通點就是它們描述的對象都是「角度大小」,因此,我們可以說:
$360^{\circ}$ 對應到的角度大小,就是 $2\pi\left.(\mathrm{rad})\right.$對應到的角度大小。
這概念相當於:
$100\left.(\mathrm{cm})\right.$對應到的長度,就是 $1\left.(\mathrm{m})\right.$對應到的長度。
因此,我們可以說:
$360^{\circ}\leftrightarrow2\pi\left.(\mathrm{rad})\right.$
值得注意的是,我這裡用到了雙箭頭符號 $\leftrightarrow$,這是因為這兩者雖然可以直接代換,但在操作或理解上就比較不自然,所以建議將兩者視為對應關係,而不是單位的換算關係。以剛才提到的弧度 $(\mathrm{rad})$ 為例,我們知道弧長 $l=25\left.\mathrm{cm}\right.$、半徑 $r=10\left.\mathrm{cm}\right.$ 與弧度 $\theta=2.5\left.(\mathrm{rad})\right.$ 滿足底下關係:
$$l\left.(\mathrm{cm})\right.=r\left.(\mathrm{cm})\right.\times\theta\left.(\mathrm{rad})\right.$$
$$25\left.(\mathrm{cm})\right.=10\left.(\mathrm{cm})\right.\times2.5\left.(\mathrm{rad})\right.$$
然而,我們能夠直接將上式的 $2.5\left.(\mathrm{rad})\right.$ 代換成與其對應的 $143.24^{\circ}$ 嗎?嗯,如剛才所說,其實是可以的,我待會會再說明。但我建議,如果要使用度數 $(^{\circ})$ 為角度單位,那麼只要將公式改成下面的模樣,一切就會好算得多。就這意義上,我建議將弧度 $(\mathrm{rad})$ 與度數 $(^{\circ})$ 當作是一種對應關係:
$$l\left.(\mathrm{cm})\right.=r\left.(\mathrm{cm})\right.\times\left[\frac{2\pi}{360}\theta\right]$$
如果我們把每一項的單位都標示清楚,其實會發現這很自然。但我還是建議,在處理物理問題時,都把角度用 $(\mathrm{rad})$ 表示。
$$l\left.(\mathrm{cm})\right.=r\left.(\mathrm{cm})\right.\times\left[\frac{2\pi}{360}\left.(\mathrm{rad}/^{\circ})\right.\theta\left.(^{\circ})\right.\right]$$
$$25\left.(\mathrm{cm})\right.=10\left.(\mathrm{cm})\right.\times\left[\frac{2\pi}{360}\left.(\mathrm{rad}/^{\circ})\right.\times143.24\left.(^{\circ})\right.\right]$$
相較於其他純粹是單位換算的場合,例如常見的自由落體末速,$V=\sqrt{2gh}$,裏頭的 $h$ 可以是公分或公尺等單位。以從高度 $h=10\left.\mathrm{m}\right.$ 位置開始自由落體,並到達地面的末速為例,
$$V=\sqrt{2gh}$$
$$\begin{align}V&=\sqrt{2\times9.8\left.\mathrm{m}/\mathrm{s}^2\right.\times10\left.\mathrm{m}\right.}\\[5pt]&=\sqrt{2\times9.8\left.\mathrm{m}/\mathrm{s}^2\right.\times1000\left.\mathrm{cm}\right.}\\[5pt]&=140\left.(\mathrm{m}\cdot\mathrm{cm}/\mathrm{s}^2)^{1/2}\right.\\[5pt]&=140\left.(0.01\left.\mathrm{m}\cdot\mathrm{m}/\mathrm{s}^2\right.)^{1/2}\right.\\[5pt]&=140\times0.1\left.\mathrm{m}/\mathrm{s}\right.\\[5pt]&=14\left.\mathrm{m}/\mathrm{s}\right.\end{align}$$
在上例中,因為我們很熟悉公分與公尺的單位換算,所以從 $(3)$ 到 $(4)$ 並沒什麼疑慮。但如果我們想在角度方面做類似的操作,其實也辦得到,只不過我們可能不太熟悉如下操作。
$$l\left.(\mathrm{cm})\right.=r\left.(\mathrm{cm})\right.\times\theta\left.(\mathrm{rad})\right.$$
$$\begin{align}l\left.(\mathrm{cm})\right.&=10\left.(\mathrm{cm})\right.\times2.5\left.(\mathrm{rad})\right.\\[5pt]&=10\left.(\mathrm{cm})\right.\times143.24\left.(^{\circ})\right.\\[5pt]&=1432.4\left.(\mathrm{cm}\cdot^{\circ})\right.\\[5pt]&=1432.4\left.(\mathrm{cm}\cdot\frac{2\pi}{360}\left.\mathrm{rad}\right.)\right.\\[5pt]&=\frac{1432.4\times2\times\left(3.1415946\cdots\right)}{360}\left.(\mathrm{cm}\cdot\mathrm{rad})\right.\\[5pt]&=25\left.(\mathrm{cm})\right.\end{align}$$
上面的 $(9)$ 其實寫得滿不自在的,更別說後面的 $(10)$ 與 $(11)$,不僅不自在也覺得很麻煩。我是第一次用上面這種方式轉換單位,更多時候我是在一開始就把轉換單位的因子 $2\pi/360$ 放入公式之中,或者都只使用以 $(\mathrm{rad})$ 為單位的各種公式。
總之,任何涉及長度的角度運算,基本上將弧度 $(\mathrm{rad})$ 做為角度單位是不會有什麼問題的。而無論如何,我們都必須在 $360$ 後方加上 $^{\circ}$,用以強調它是另一種角度單位。倘若沒有加上 $^{\circ}$,那可能會讓人誤以為 $2\pi\left.(\mathrm{rad})\right.$等同於 $360$ 的數字,就好像 $3\left.(\mathrm{m})\right.=300$,這是不妥當的。甚至有人也會跟著省略 $\left.(\mathrm{rad})\right.$,變成了 $2\pi = 360$。然而,這就又會使人忘記 $\pi$ 這個數字與長度的關係,而且那種關係也不太能是某種 $180$ 倍的關係。
廣義而言,我們能簡單得出以下兩個關係:
$1\left.(^{\circ})\right.\leftrightarrow\pi/180\left.(\mathrm{rad})\right.=0.01745\cdots\left.(\mathrm{rad})\right.$
$1\left.(\mathrm{rad})\right.\leftrightarrow180/\pi\left.(^{\circ})\right.=57.296\left.(^{\circ})\right.$
也就是說,以前為了方便整除而制定的 $1^{\circ}$,其張開的弧長與半徑的比值會是 $0.01745\cdots$。又或者,現今制定的 $1\left.(\mathrm{rad})\right.$相當於過去的 $57.296^{\circ}$!