物理學的發展，原則上就是盡可能地化繁為簡。能夠用一句話說清楚的，就不要用兩句話來說。如果可能，我們希望這世界的運作機制能夠僅由一條簡單的定律來解釋。常見的溫度與熱，是不是可以用我們更熟悉的日常現象來解釋呢？在我們學完溫度以及基本的熱現象後，我們往往緊接著學習所謂的氣體動力論（Kinetic theory of gas），之所以如此，是因為這能讓我們進一步了解常見的熱現象究竟是怎麼來的。

氣體動力論的主要內容是，氣體就是朝四面八方運動的粒子，而氣壓就是這些粒子撞擊器壁造成的。簡言之，它的嘗試讓我們能夠將抽象的但巨觀的「熱現象」理解為「微觀的粒子運動」——常見的自然現象：粒子的運動。倘若我們能使用粒子運動解釋熱現象，那就這意義上，我們將「熱現象」化約為「粒子運動」的問題了。這對於牛頓力學而言是很好的，因為這讓牛頓力學能應用的範圍更加廣大了。此外，在所有可能假設的、考慮的模型中，這種「粒子間作用力可忽略」的情況——氣體——是最容易考慮的，因為其他的情況太複雜了（如固體、液體等）。話說回來，雖然在所有高中以及大學物理課本中，都有氣體動力論的詳細推導過程，但這些推導都會涉及所謂的平均力，例如：

$$F_{\text{avg}}=\sum_{i=1}^N\left(\frac{2mv_{i,x}}{2L/v_{i,x}}\right)$$

但這裡的平均力 $F_{\text{avg}}$ 究竟是不是瞬時力呢？畢竟，我們只能測量到瞬時力造成的壓力。由於我們並不是由瞬時力 $F(t)$ 開始推導，而是先將每個粒子施力平均後，再加總得出平均力，所以不免讓部分同學感到這時的平均有點「任意」、「天外飛來一筆」。此外，這樣的推導過程難免讓人感到有點不真實。畢竟，我們測量到的壓力，都不是平均的，而是瞬時力對面積的比值。

有鑑於此，我嘗試從有別於傳統教科書（包括大學普物課本，Halliday & Serway）的角度，從瞬時力開始推導，並詳盡說明所謂的「平均」意義。這樣推導的好處是，至少可以破除「要累積一段時間動量之後，才能平均算出這個力量 / 氣體壓力」的相關迷思。這推導讓我們從力量的疊加性開始思考，而非毫無緣由地，以 $\Delta t_i=2L/v_{i,x}$ 的時距，計算所謂的平均力，然後再把這些不同時段下考慮的平均力加總起來。在我的推導中，不會強調、凸顯 $2mv_x / (2L/v_x)$ 這項為平均力，因為它只會是個計算過程中的一項而已。當然，如果你尚未學過氣體動力論，那麼其實並不需要了解上述想法，只需要繼續往下看就好囉。

---

氣體動力論的基本近似是：

1. 【零體積近似】：氣體直徑 $d$ 對容器邊長 $L$ 的比值近似為零， $0<d/L\ll 1$。我們也可將此理解為氣體粒子的體積要多小就有多小。
2. 【氣體透明近似】：粒子之間碰撞機率近似為零，亦即它們總是穿透彼此，對彼此而言是透明的（最後會評論此近似）。而氣體粒子只會受到它與器壁間的碰撞作用。
3. 【能量守恆近似】：碰撞時損失的力學能比例近似為零，$\Delta E_k/E_{k,i}\approx 0$。換言之，所有的碰撞都是彈性碰撞。

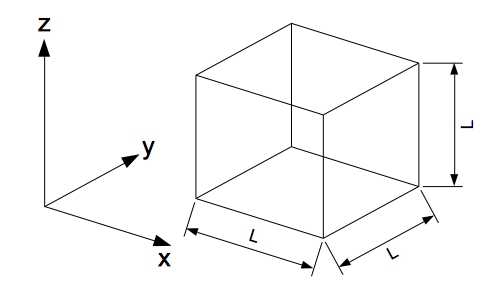
首先，讓我說清楚我們處理的物理情境。有個邊長為 $L$ 的正立方形盒子，裡面的氣體總數為 $N$，每個粒子都以四面八方、非常亂的方式在互相碰撞著。

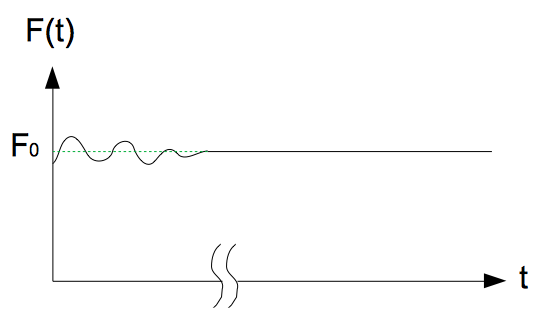
不論這氣體系統是如何製備的，在經歷足夠長的時間後，我們不難發現此時壓力處處相同。我們說，此時系統已達熱平衡。換言之，對一特定器壁而言，在足夠長時間後，器壁所受氣體之撞擊力對時間而言將會是個常數函數，我們將它定為 $F_0$。

$$F(t)=F_0\tag{1}$$

這個力量是怎麼來的呢？根據我們的模型，我們知道這力量是源自時間在 $t$ 時，那些正在與器壁碰撞的粒子們所施予的力量 $F_i(t)$，也就是說：

$$F(t)=\sum_{i=1}^N F_i(t)\tag{2}$$

特別注意的是，此時並不是所有的粒子都正在跟該器壁碰撞。還有許許多多的粒子正在飛行著，因此，有些粒子對器壁的撞擊力是零，有些不是。

$$\begin{cases}F_i(t)\neq0,&\text{  if it’s during collision;}\\[2ex]F_i(t)=0,&\text{  if it’s not during collision.}\end{cases}\tag{3}$$

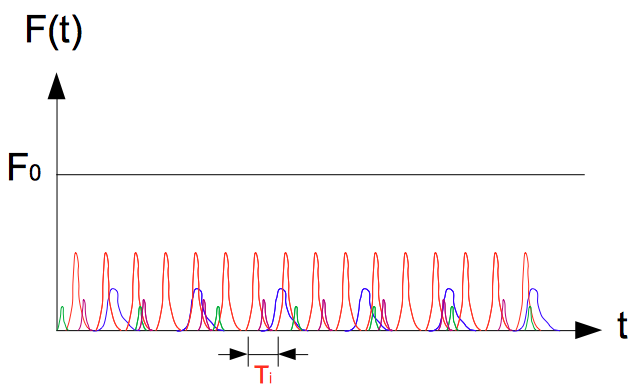
雖然每個粒子的速度都不同，而且也不是每個粒子都同時（一起）撞擊器壁，但因為它們互相穿透彼此，所以當粒子與器壁碰撞結束後，就會以 $x$ 方向上等速度運動的方式，到達下一個 $yz$ 平面的器壁，然後又以反向同速率的運動回到最初的器壁。因此，每個粒子對該器壁的碰撞具有一定的規律：每個粒子對器壁的撞擊週期為 $T_i$。

$$T_i=\frac{2L}{v_{i,x}}\tag{4}$$

因此，我們可以藉由下圖解釋恆定力量 $F(t)=F_0$ 的由來。

還記得先前提到的 $F(t)=\sum_{i=1}^N F_i(t)$，雖然並不是每個粒子時時刻刻都在跟該器壁碰撞，但很神奇的是，達熱平衡時，任何時候的碰撞總力道居然會是相同的 $F_0$。為了考慮每個粒子的碰撞，我們重新改寫器壁受力 $F(t)$ 為：

$$F(t)=\frac{F(t)\times T}{T}\tag{5}\label{5}$$

這裡的 $T$ 被粗略地定義為所有粒子之碰撞週期 $T_i$ 數值的乘積。值得注意的是，$T$ 的單位仍然是 $\left.\mathrm{s}\right.$，而非 $\left.\mathrm{s}^N\right.$。待會就清楚為什麼我們如此定義 $T$ 了。而在最後面的分析與討論，我也會說明 (a) 如何以任意時段 $T$ 來推導以及 (b) 如何更精確地定義 $T$：

$$T\equiv T_1\;T_2\;T_3\;\cdots T_N\tag{6}\label{6}$$

接著，因為此時系統已達熱平衡，所以方程式 $(\ref{5})$ 的分子即恰好為器壁在時距 $T$ 中，氣體粒子對器壁施予的衝量總和：

$$F(t)=\frac{\sum_{i=1}^N J_i(T)}{T}\tag{7}$$

現在的問題就是，第 $i$ 個粒子在 $T$ 的時距中，究竟給牆壁多少的衝量？由於我們在方程式 $(\ref{6})$ 中的 $T$ 定義，以及第 $i$ 個粒子每經歷一次 $T_i$ 時距，就會因著彈性碰撞的假設而施予器壁 $2mv_{i,x}$ 的衝量，因此，第 $i$ 個粒子在 $T$ 時距中，跟器壁碰撞的次數 $n_i$ 為：

$$n_i\equiv\frac{T}{T_i}=T_1\;T_2\cdots T_{i-1}\;T_{i+1}\cdots T_N\tag{8}\label{8}$$

因此，我們可知器壁所受的瞬時力 $F(t)$ 為：

$$\begin{align}F(t)&=\frac{\sum_{i=1}^N J_i(T)}{T}\tag{9a}\label{9a}\\[4ex]&=\frac{\sum_{i=1}^N n_i(2mv_{i,x})}{T}\tag{9b}\label{9b}\\[4ex]&=\sum_{i=1}^N \left(\frac{n_i}{T}\right)\left(2mv_{i,x}\right)\tag{9c}\label{9c}\\[4ex]&=\sum_{i=1}^N\left(\frac{1}{T_i}\right)\left(2mv_{i,x}\right)\tag{9d}\label{9d}\\[4ex]&=\sum_{i=1}^N\frac{2mv_{i,x}}{2L/v_{i,x}}\tag{9e}\label{9e}\\[4ex]&=\sum_{i=1}^N\frac{mv_{i,x}^2}{L}\tag{9f}\label{9f}\end{align}$$

在方程式 $(\ref{9c})$ 推到 $(\ref{9d})$ 的過程中，我們用到了撞擊次數 $n_i$ 的定義式 $(\ref{8})$。最後，我們就可得出施加在該器壁的壓力了！在此我們用到面積 $A=L^2$ 的條件。

$$P\equiv\frac{F(t)}{A}=\frac{\sum_{i=1}^N mv_{i,x}^2}{L^3}\tag{10}\label{10}$$

接下來，我們可以用同樣的推論，針對 $xy$ 平面上的器壁、$xz$ 平面上的器壁做如上分析，我們即可得到下列的各向同性結果。

$$P=\frac{\sum_{i=1}^N mv_{i,y}^2}{L^3}=\frac{\sum_{i=1}^N mv_{i,z}^2}{L^3}\tag{11}\label{11}$$

$$\therefore\sum_{i=1}^N v_{i,x}^2=\sum_{i=1}^N v_{i,y}^2=\sum_{i=1}^N v_{i,z}^2\tag{12}\label{12}$$

又因為畢氏定理 $v_i^2=v_{i,x}^2+v_{i,y}^2+v_{i,z}^2$，所以可得

$$\sum_{i=1}^N v_{i,x}^2+\sum_{i=1}^N v_{i,y}^2+\sum_{i=1}^N v_{i,z}^2=\sum_{i=1}^N v_{i}^2\tag{13}\label{13}$$

同時考慮方程式 $(\ref{12})$、$(\ref{13})$ 後，可以得出

$$3\sum_{i=1}^N v_{i,x}^2=\sum_{i=1}^N v_i^2\quad\to\quad\sum_{i=1}^N v_{i,x}^2=\frac{1}{3}\sum_{i=1}^N v_i^2\tag{14}$$

因此，倘若我們定義容器體積 $V\equiv L^3$，那麼即可將方程式 $(\ref{10})$ 的壓力 $P$ 改寫為：

$$PV=\frac{1}{3}\sum_{i=1}^N mv_i^2\tag{15}$$

換言之，我們知道了由 $N$ 個質點粒子組成的氣體系統總動能與 $PV$ 的關係為：

$$E_{k\text{, total}}=\sum_{i=1}^N \frac{1}{2}mv_{i}^2=\frac{3}{2}PV\tag{16}$$

搭配理想氣體方程式 $PV=Nk_{B}T$，我們會得到十分振奮人心的結果：

$$E_{k\text{, total}}=\frac{3}{2}Nk_B T\quad\to\quad\bar{E}_{k}=\frac{3}{2}k_B T\tag{17}\label{17}$$

就這方程式 $(\ref{17})$ 的意義上，我們可以說，物體之溫度是其微觀動能的巨觀呈現。而這樣的解釋正確嗎？我們如何驗證呢？氣體動力論的一個重要理論結果就在於其定體積莫耳熱容量 $c_v$：

$$c_v(T)\equiv\frac{1}{n}\frac{dQ_v}{dT}\tag{18}$$

其中，$dQ_v/dT$ 為系統在定體積條件下，在溫度 $T$ 時，系統對溫度的吸熱率（$\left.\mathrm{J}\middle/\mathrm{K}\right.$），且當外界透過熱交互作用給系統能量時，$dQ>0$。根據能量守恆定律（許多人叫它熱力學第一定律）：

$$\Delta E=Q+W\tag{19}$$

其中，若外界透過作功的方式將能量傳遞給系統時，$W>0$。我們可知在定體積情況，外界不對系統作功（器壁完全沒有位移），所以 $dQ_v=dE$。又因為理想氣體系統之總能量（許多人說它是內能，但我說是總能量）為

$$E=E_{k,\text{ total}}=\frac{3}{2}nRT\tag{20}$$

因此，我們可得，當理想氣體系統在定體積之熱力學過程時，其莫耳熱容量 $c_v$ 為

$$c_v=\frac{3}{2}R=\frac{3}{2}\left(8.314\left.\mathrm{J}\middle/\mathrm{mol}\cdot\mathrm{K}\right.\right)\approx 12.471\left.\mathrm{J}\middle/\mathrm{mol}\cdot\mathrm{K}\right.\tag{21}$$

由這關鍵的數字——而且還是獨立於溫度的常數！——讓我們可藉由實驗來驗證上述理論究竟有多大程度的正確性。而實驗告訴我們單原子氣體 He、Ne、Ar、Kr 的定體積莫耳熱容量 $c_v$ 分別為 $12.5$、$12.5$、$12.7$、$12.3 \left.\mathrm{J}\middle/\mathrm{mol}\cdot\mathrm{K}\right.$（抄自 Serway 普通物理第九版），由此可知氣體動力論十分準確。

---

進一步的分析與討論

1. $\Delta t_i=2L/v_{i, x}$ 的意義

由此可更加確定為什麼我們需要用 $\Delta t_i=2L/v_{i, x}$ 來計算「平均力量」，這是因為當我們將瞬時力 $F(t)$ 改寫為 $[F(t)T]/T$ 時，我們相當於用平均力的角度去詮釋瞬時力。而這兩者在熱平衡的條件下，確實是相同的。另外，在許多物理教材中提及的下式

$$P=\frac{F_x}{L^2}=\frac{mv_{x1}^2/L+mv_{x2}^2/L+\cdots+mv_{xN}^2/L}{L^2}\tag{22}$$

其實是方程式 $(\ref{9a})$ 至 $(\ref{9f})$ 的結果，只有在考慮 $T$ 為所有碰撞週期 $T_i$ 之公倍數（不需為最小）時，才能夠簡單計算出這結果。

2. 以任意時段為 $T$

如果不將 $T$ 定義為所有碰撞週期 $T_i$ 之公倍數，那麼雖然會稍微麻煩一點，但還是會有一樣的結果。例如，如果我們把 $T$ 定義為比任何碰撞週期 $T_i$ 還要小的話，這時雖然只有部分粒子會在時距 $T$ 內撞擊，但這些粒子所傳遞給器壁的衝量，與在時距 $T_1\;T_2\cdots T_N$ 內傳遞的衝量必定會跟兩段時距長度成正比。這是由於已達熱平衡，瞬時力即平均力，所以對於任意兩時距 $\Delta t_1$ 與 $\Delta t_2$ 而言，氣體對器壁施予的衝量比值恰好為時距比：

$$\frac{\sum_{i=1}^N J_i(\Delta t_1)}{\sum_{i=1}^N J_i(\Delta t_2)}=\frac{\int_{t_{1,i}}^{t_{1,i}+\Delta t_1} F(t)dt}{\int_{t_{2,i}}^{t_{2,i}+\Delta t_2} F(t)dt}=\frac{F_0\Delta t_1}{F_0\Delta t_2}=\frac{\Delta t_1}{\Delta t_2}\tag{23}$$

因此，我們的瞬時力即為（底下的 $T$ 為任意值）：

$$\begin{align}F(t)&=\frac{\sum_{i=1}^N J_i(T)}{T}\tag{24a}\\[4ex]&=\left[\frac{\sum_{i=1}^N J_i(T)}{\sum_{i=1}^N J_i(T_1\;T_2\cdots T_N)}\right]\frac{\sum_{i=1}^N J_i(T_1\;T_2\cdots T_N)}{T}\tag{24b}\\[4ex]&=\left[\frac{T}{T_1\;T_2\cdots T_N}\right]\frac{\sum_{i=1}^N J_i(T_1\;T_2\cdots T_N)}{T}\tag{24c}\\[4ex]&=\frac{\sum_{i=1}^N J_i(T_1\;T_2\cdots T_N)}{T_1\;T_2\cdots T_N}\tag{24d}\end{align}$$

如此一來，我們就會得到跟原先方程式 $(\ref{9a})$ 的結果，因此不論我們考慮多長的時間 $T$，都能夠計算出相同的器壁瞬時受力。

3. 嚴謹定義 $T$ 與 $n_i$

先前的 $T$ 定義有兩個麻煩：(a) 不自然的單位以及 (b) 碰撞次數 $n_i$ 顯然不是整數。我們可以任意設定兩個碰撞週期來說明這兩點。例如，以只有兩個粒子，$T_1 = 0.12\left.\mathrm{s}\right.$、$T_2 = 0.07\left.\mathrm{s}\right.$ 為例。難道 1 號粒子的碰撞次數為 0.07 次嗎？

$$n_1=\frac{T}{T_1}=\frac{T_1\;T_2}{T_1}=T_2=0.07\tag{25}$$

再者，既然 $T$ 都定義為 $T\equiv T_1T_2$，那麼 $T$ 的單位不就應該是 $\left.\mathrm{s}^2\right.$ 嗎？為了解決這兩個困擾，我們可以任意設定一個足夠小的時間單位 $T_s$，使得所有粒子的碰撞週期都恰好是它的整數倍。例如，我們能設定 1 毫秒為新的時間單位 $T_s\equiv 1\left.\mathrm{ms}\right.$，再將 $T$ 重新定義為：

$$T\equiv\left[\left(\frac{T_1}{T_s}\right)\left(\frac{T_2}{T_s}\right)\cdots\left(\frac{T_N}{T_s}\right)\right]T_s=\left(\prod_{i=1}^{N}\frac{T_i}{T_s}\right)\;T_s\tag{26}$$

以先前的 $T_1=0.12\left.\mathrm{s}\right.$、$T_2=0.07\left.\mathrm{s}\right.$ 例子而言，我們在方程式 $(\ref{9a})$ 中考慮的足夠長的時間 $T$ 則為：

$$\begin{align}T&=\left[\left(\frac{T_1}{T_s}\right)\left(\frac{T_2}{T_s}\right)\right]T_s\tag{27a}\\[4ex]&=\left[\left(\frac{0.12\left.\mathrm{s}\right.}{1\left.\mathrm{ms}\right.}\right)\left(\frac{0.07\left.\mathrm{s}\right.}{1\left.\mathrm{ms}\right.}\right)\right]T_s\tag{27b}\\[4ex]&=\left( 120\cdot 70 \right)\cdot\left(1\left.\mathrm{ms}\right.\right)\tag{27c}\\[4ex]&=8400\left.\mathrm{ms}\right.\tag{27d}\end{align}$$

而在將碰撞週期 $T_i$ 改為以 $T_s$ 為單位後（例：$T_1=0.12\left.\mathrm{s}\right.=120\left.\mathrm{ms}\right.$），碰撞次數 $n_i$ 則定義為

$\begin{align}n_i&\equiv \frac{T}{T_i}\tag{28a}\\[4ex]&=\left(\frac{T_1\;T_2\cdots T_N}{T_s^N}\;T_s\right)\frac{1}{T_i}\tag{28b}\\[4ex]&=\frac{T_1\cdots T_{i-1}\;T_{i+1}\cdots T_N}{T_s^{N-1}}\tag{28c}\\[4ex]&=\left(\frac{T_1}{T_s}\right)\left(\frac{T_2}{T_s}\right)\cdots\left(\frac{T_{i-1}}{T_s}\right)\left(\frac{T_{i+1}}{T_s}\right)\cdots\left(\frac{T_N}{T_s}\right)T_s\tag{28d}\end{align}$

因此，在 $T_1=0.12\left.\mathrm{s}\right.$、$T_2=0.07\left.\mathrm{s}\right.$ 例子中，

$$\begin{align}n_1&=\frac{T}{T_1}\tag{29a}\\[4ex]&=\frac{8400\left.\mathrm{ms}\right.}{120\left.\mathrm{ms}\right.}\tag{29b}\\[4ex]&=70\tag{29c}\end{align}$$

如此一來，在計算方程式 $(\ref{9a})$ 至 $(\ref{9b})$ 時，就不會感到怪怪的。

$$\frac{\sum_{i=1}^N J_i(T)}{T}=\frac{\sum_{i=1}^N n_i\left(2mv_{i,x}\right)}{T}\tag{9a – b}$$

4. 氣體透明近似

接著我們談談先前的「氣體透明近似」。雖然我們將各氣體粒子之間的碰撞機率近似為零，也就是說，它們是互相透明的，但假如我們考慮氣體的平均自由徑（平均每兩次碰撞之間，氣體粒子做直線運動的行走距離）：

$$\lambda = \frac{1}{\sqrt{2}n\pi d^2}\tag{30}$$

其中，$n\equiv N/L^3$，即為氣體粒子數量密度，而 $d$ 則為氣體粒子直徑。倘若 $\lambda > L$，那就是說，氣體粒子在互相撞擊之前，就會先與器壁碰撞。因此，「氣體粒子之間是互相透明的」就是合理的近似。因此，

$$\lambda > L\quad\to\quad N<\frac{L^2}{\sqrt{2}\pi d^2}\tag{31}$$

在氣體直徑要多小就有多小的前提下，我們可得

$$N<\lim_{d\to 0}\frac{L^2}{\sqrt{2}\pi d^2}=\infty\tag{32}\label{32}$$

由於上式 $(\ref{32})$ 顯然總是成立，所以，原則上，我們就算不特別將氣體粒子碰撞機率近似為零——氣體粒子是透明的——也是合理的。換言之，零體積近似，某種程度上，邏輯蘊涵了透明氣體近似。先前之所以特別強調透明近似，是因為可避開在最一開始就提平均自由徑的概念。總而言之，只要氣體粒子直徑對容器邊長的比值趨於零 $d/L\to0$，那麼它們碰撞到彼此的機率顯然就也趨於零。如此一來，理想氣體的粒子對器壁的碰撞就確實具有週期性，週期 $T_i=2L/v_{i,x}$，也就可以合理地使用下式評估氣體粒子施予器壁的衝量。

$$J_i(T_1\;T_2\cdots T_N)=n_i\left(2mv_{i,x}\right)\tag{33}$$

以凡德瓦直徑為 $280\left.\mathrm{pm}\right.$ 的氦氣 He 作為氣體粒子直徑 $d$ 為例，那麼在 $\lambda < L$ 且邊長 $L=30\left.\mathrm{cm}\right.$ 的容器的情況下：

$$N<\frac{L^2}{\sqrt{2}\pi d^2}=\frac{\left(30\left.\mathrm{cm}\right.\right)^2}{\sqrt{2}\pi\cdot \left(280\cdot 10^{-12}\left.\mathrm{m}\right.\right)^2}\approx 2.58\times 10^{17}\tag{34}$$

換言之，大概要讓氣體粒子數目在 $N/N_A = 3.74\times 10^{-7}\left.\mathrm{mol}\right.$ 以下，就是氦氣 He 質量必須小於 $1.72\times 10^{-6}\left.\mathrm{g}\right.=1.72\left.\mathrm{\mu g}\right.$，才能夠合理地在不考慮氦氣 He 粒子間碰撞的前提下，得出氦氣 He 粒子對器壁作週期性地碰撞的結論。

5. 三維彈性碰撞

而如果要考慮氣體粒子的碰撞，那麼由於我們需要求出兩粒子的末速度，所以就有六個未知數 $v_{1,fx}$、$v_{1,fy}$、$v_{1,fz}$、$v_{2,fx}$、$v_{2,fy}$、$v_{2,fz}$。然而，根據動量與能量守恆，我們卻只能得出底下四條方程式：

$$m_1v_{1,ix}+m_2v_{2,ix}=m_1v_{1,fx}+m_2v_{2,fx}\tag{35a}$$

$$m_1v_{1,iy}+m_2v_{2,iy}=m_1v_{1,fy}+m_2v_{2,fy}\tag{35b}$$

$$m_1v_{1,iz}+m_2v_{2,iz}=m_1v_{1,fz}+m_2v_{2,fz}\tag{35c}$$

$$\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1v_{1,f}^2+\frac{1}{2}m_2v_{2,f}^2\tag{35d}$$

因此，除非我們進一步假設碰撞的微觀機制，例如說，如何地考慮正向力或摩擦力等，然後再補上兩條方程式（可能是力矩、角動量守恆等），這樣才能求出三維碰撞末速。但其實基於上述的平均自由徑考慮，絕大多數的粒子是幾乎不會撞擊到彼此的。

---